A ![]() di una soluzione
di una soluzione
![]() in acido
benzoico (
in acido
benzoico (![]() ) e
) e ![]() in benzoato di sodio
(
in benzoato di sodio
(![]() ) vengono aggiunti
) vengono aggiunti ![]() di una soluzione
di
di una soluzione
di ![]()
![]() . Determinare il
. Determinare il ![]() della soluzione prima e
dopo l'aggiunta.
della soluzione prima e
dopo l'aggiunta.
![]()
Dati:
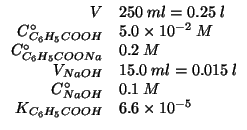
La soluzione in esame contiene un acido debole e la sua base coniugata
(proveniente dalla dissociazione totale del benzoato sodico,
elettrolita forte) in concentrazioni apprezzabili: si tratta quindi di
una soluzione tampone.
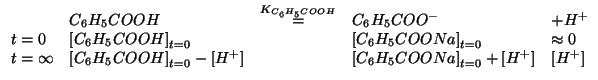
Le concentrazioni di equilibrio devono soddisfare la legge dell'azione
di massa:
Dato il valore piccolo di
![]() e la presenza di
un'apprezzabile concentrazione iniziale dell'anione
dell'acido, si puo' assumere in prima
approssimazione che la reazione sia poco spostata verso destra: cio'
consente di trascurare
e la presenza di
un'apprezzabile concentrazione iniziale dell'anione
dell'acido, si puo' assumere in prima
approssimazione che la reazione sia poco spostata verso destra: cio'
consente di trascurare
![]() come addendo nella legge
dell'azione di massa. In modo conciso:
come addendo nella legge
dell'azione di massa. In modo conciso:
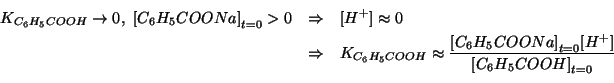
Si puo' quindi ricavare facilmente il ![]() cercato:
cercato:
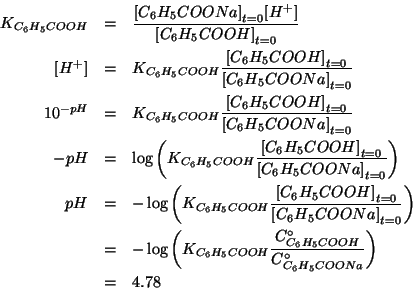
Osserviamo che:
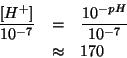
e quindi l'approssimazione circa l'autoionizzazione dell'acqua e' accettabile.
Inoltre:
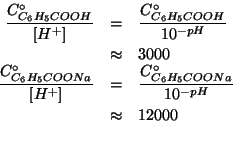
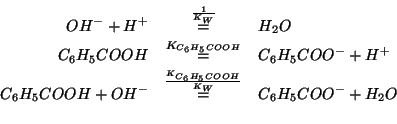
La reazione globale si puo' trattare nel modo usuale per il calcolo
del ![]() . Prendendo la concentrazione di equilibrio degli ioni
ossidrile come incognita si ha:
. Prendendo la concentrazione di equilibrio degli ioni
ossidrile come incognita si ha:
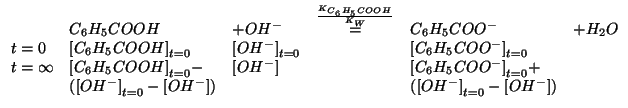
Le concentrazioni di equilibrio devono soddisfare la legge dell'azione
di massa:
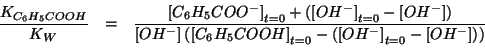
A questo punto, si puo' osservare che il valore del rapporto
![]() e' molto grande (dell'ordine di
e' molto grande (dell'ordine di ![]() )
e quindi la reazione si puo' considerare completa. In tale ipotesi si
deve stabilire qual'e' il reagente limitante: se il reagente limitante
e'
)
e quindi la reazione si puo' considerare completa. In tale ipotesi si
deve stabilire qual'e' il reagente limitante: se il reagente limitante
e' ![]() , allora la concentrazione di equilibrio degli ioni
ossidrile si puo' assumere nulla, se invece il reagente limitante e'
, allora la concentrazione di equilibrio degli ioni
ossidrile si puo' assumere nulla, se invece il reagente limitante e'
![]() , allora rimarranno degli ioni ossidrile non reagiti,
in concentrazione pari a
, allora rimarranno degli ioni ossidrile non reagiti,
in concentrazione pari a
![]() .
In modo conciso:
.
In modo conciso:
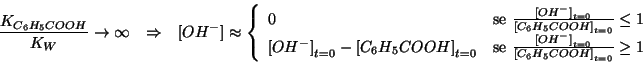
Per il calcolo delle concentrazioni iniziali bisogna tenere conto
della diluizione provocata dall'aggiunta della soluzione di ![]() :
:
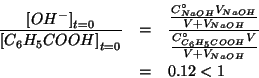
Il reagente limitante e' dunque ![]() . Quindi si puo'
assumere:
. Quindi si puo'
assumere:
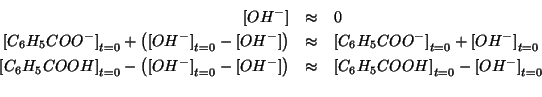
La legge dell'azione di massa si semplifica in:

Osserviamo che il ![]() dopo l'aggiunta e' aumentato, come e' logico
aspettarsi, visto che si e' aggiunta una base forte. D'altro canto,
l'aumento di
dopo l'aggiunta e' aumentato, come e' logico
aspettarsi, visto che si e' aggiunta una base forte. D'altro canto,
l'aumento di ![]() e' contenuto, come conseguenza dell'effetto
tampone.
e' contenuto, come conseguenza dell'effetto
tampone.
Infine:
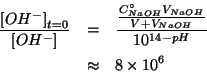
da cui si deduce che le approssimazioni:
sono appropriate.
Calcolare quanti chilogrammi di monossido di carbonio e di diossido di
zolfo si possono ottenere dalla combustione di una tonnellata
(![]() ) di un carbone che contiene il
) di un carbone che contiene il ![]() di
carbonio e lo
di
carbonio e lo ![]() di zolfo, se la resa e' pari al
di zolfo, se la resa e' pari al
![]() . Determinare inoltre quanti chilogrammi di ossigeno sono
necessari.
. Determinare inoltre quanti chilogrammi di ossigeno sono
necessari.
Dati:
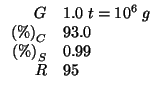
Altri simboli:
| massimo numero di moli di |
|
| massimo numero di moli di |
|
| numero di moli di |
|
| numero di moli di |
|
| numero di moli di |
|
| numero di moli di |
|
| numero di moli di |
|
| massa di |
|
| massa di |
|
| massa di |
|
| massa di |
|
| massa di |
|
| massa molare di |
|
| massa molare di |
|
| massa molare di |
|
| massa molare di |
|
| massa molare di |
Le due reazioni di combustione sono:
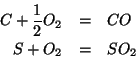
Per ![]() si ha:
si ha:
dove il fattore ![]() deriva dalla conversione
deriva dalla conversione
![]() . Il numero di moli di
. Il numero di moli di ![]() ottenute si puo'
esprimere in funzione del numero massimo ottenibile e della resa:
ottenute si puo'
esprimere in funzione del numero massimo ottenibile e della resa:
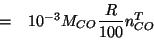
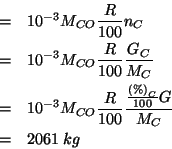
In modo identico, per ![]() si ha:
si ha:
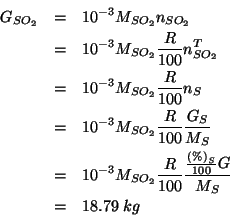
La quantita' di ossigeno necessaria viene calcolata sulla base della
stechiometria delle due reazioni di combustione e del numero iniziale di moli
di ![]() e
e ![]() .
.
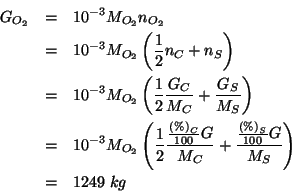
Calcolare il numero di ioni in cui si dissocia un sale di massa molare
![]() sapendo che una soluzione di
sapendo che una soluzione di ![]() di sale in
di sale in
![]() di
di ![]() ha un abbassamento del punto di congelamento
pari a
ha un abbassamento del punto di congelamento
pari a ![]() . La costante crioscopica dell'acqua vale
. La costante crioscopica dell'acqua vale
![]() .
.
Dati:
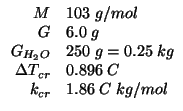
Altri simboli:
| numero di ioni generati dal sale | |
| molalita' formale del sale | |
| numero di moli di sale |
Dalla relazione che da' l'abbassamento crioscopico per una soluzione
di data molalita', tenendo conto che il sale si dissocia completamente
in ![]() ioni:
ioni:
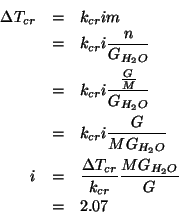
Si puo' quindi concludere che il sale si dissocia in due ioni:
![]()