Sapendo che a una certa temperatura e pressione l'entalpia di
combustione di ![]() e'
e'
![]() e che le entalpie
di formazione di
e che le entalpie
di formazione di ![]() e
e ![]() sono rispettivamente
sono rispettivamente
![]() e
e
![]() , calcolare l'entalpia di
formazione di
, calcolare l'entalpia di
formazione di ![]() nelle stesse condizioni.
nelle stesse condizioni.
Dati:

La reazione di formazione di ![]() e':
e':
![]()
Questa reazione puo' essere scritta come somma delle seguenti reazioni di cui si conosce la variazione di entalpia:
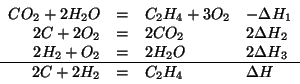
A questo punto, ricordando che l'entalpia e' una funzione di stato, si ha:
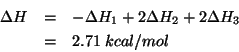
Calcolare quanti grammi di formiato sodico (![]() ) occorre sciogliere in
) occorre sciogliere in
![]() di una soluzione
di una soluzione ![]() di acido formico (
di acido formico (![]() ) per
rendere la concentrazione degli ioni idrogeno
) per
rendere la concentrazione degli ioni idrogeno ![]() volte minore.
volte minore.
(
![]() )
)
Dati:
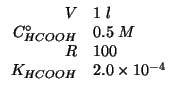
Altri simboli:
|
|
concentrazione di ioni |
| massa di |
|
| massa molare di |
|
| numero di moli di |
La reazione di ionizzazione dell'acido formico e':
![]()
Questa reazione verra' spostata verso sinistra dall'aggiunta del sale
(che genera una quantita' stechiometrica di ioni ![]() ) per il
principio di Le Chatelier. Si tratta quindi di stabilire quanto sale
si deve aggiungere affinche' lo spostamento dell'equilibrio di
ionizzazione sia tale da rendere la concentrazione di ioni
) per il
principio di Le Chatelier. Si tratta quindi di stabilire quanto sale
si deve aggiungere affinche' lo spostamento dell'equilibrio di
ionizzazione sia tale da rendere la concentrazione di ioni ![]() pari a
pari a ![]() di quella esistente prima dell'aggiunta.
di quella esistente prima dell'aggiunta.
Risulta piu' comodo considerare una condizione iniziale in cui si ha solo l'acido indissociato e la sua base coniugata: cio' e' lecito in quanto la condizione finale raggiunta dal sistema e' indipendente dalla particolare condizione di partenza, purche' la composizione globale sia sempre la stessa.
Impostiamo la trattazione usuale dell'equilibrio, trascurando l'autoionizzazione dell'acqua:

Le concentrazioni di equilibrio devono soddisfare la legge dell'azione
di massa:
A questo punto, il problema e' trovare
![]() sapendo che deve essere
sapendo che deve essere
![]() :
:
Si deve ora trovare
![]() . A questo scopo, consideriamo
lo stesso equilibrio di ionizzazione, ma senza la presenza di una
concentrazione iniziale di ione
. A questo scopo, consideriamo
lo stesso equilibrio di ionizzazione, ma senza la presenza di una
concentrazione iniziale di ione ![]() :
:
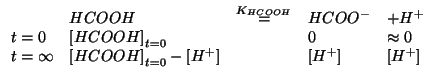
Considerato il valore piccolo di ![]() , possiamo trascurare
in prima approssimazione la quantita' di acido che si dissocia. In
altri termini:
, possiamo trascurare
in prima approssimazione la quantita' di acido che si dissocia. In
altri termini:
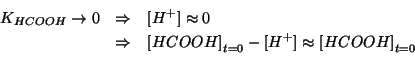
e quindi:
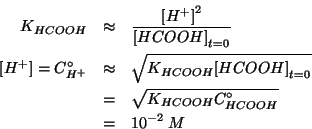
Notiamo che, mentre trascurare gli ioni idronio provenienti
dall'autoionizzazione dell'acqua appare perfettamente lecito, il
valore trovato e' solo ![]() volte piu' piccolo della concentrazione
iniziale di acido. Cio' suggerisce che l'approssimazione
volte piu' piccolo della concentrazione
iniziale di acido. Cio' suggerisce che l'approssimazione
![]() potrebbe non essere valida.
potrebbe non essere valida.
Risolviamo allora l'equazione quadratica che si ottiene considerando
la legge dell'azione di massa (equazione ![]() ) senza
semplificazioni:
) senza
semplificazioni:
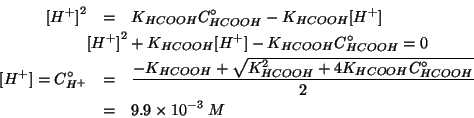
Il valore cosi' ottenuto puo' ora essere inserito
nell'espressione ![]() . Si ha cosi':
. Si ha cosi':
Infine, siccome e' richiesta la quantita' di ![]() in grammi:
in grammi:
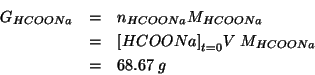
Lo ione ![]() forma un addotto acido base di Lewis con
l'ammoniaca secondo:
forma un addotto acido base di Lewis con
l'ammoniaca secondo:
Determinare la costante di equilibrio relativa alla reazione su
scritta sapendo che il potenziale elettrodico di una semicella
costituita da un filo di ![]() immerso in una soluzione contenente
concentrazioni iniziali di
immerso in una soluzione contenente
concentrazioni iniziali di ![]() e
e ![]() ripettivamente
pari a
ripettivamente
pari a ![]() e
e ![]() risulta
risulta ![]() alla temperatura di
alla temperatura di
![]() .
.
(
![]() )
)
Dati:
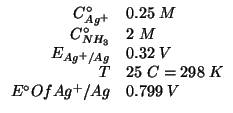
Altri simboli:
| costante di Faraday: |
|
| costante dei gas:
|
Consideriamo l'equilibrio di formazione dell'addotto:
![$
\begin{array}{lllll}
&{Ag^+}&+2{NH_3}&=&\left[Ag({NH_3})_2\right]^+\\
t=0&\In...
...{Ag^+}}-\ConcOf{{Ag^+}}}&&\InitialConcOf{{Ag^+}}-\ConcOf{{Ag^+}}\\
\end{array}$](img64.gif)
La costante di equilibrio cercata e' data da:
La concentrazione di equilibrio degli ioni ![]() si ricava dal
potenziale elettrodico tramite la legge di Nernst:
si ricava dal
potenziale elettrodico tramite la legge di Nernst:
![]()
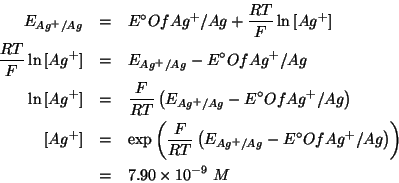
Sostituendo nell'equazione ![]() si ottiene:
si ottiene: