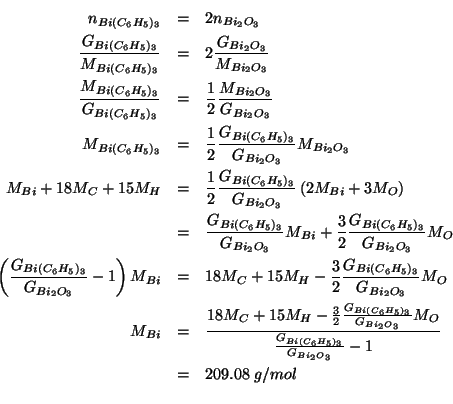La percentuale in massa di ![]() in un campione di piombo contenente
in un campione di piombo contenente
![]() come impurezza venne determinata come segue. Una massa di
come impurezza venne determinata come segue. Una massa di
![]() di piombo venne sciolta in acido nitrico per produrre
di piombo venne sciolta in acido nitrico per produrre
![]() e
e
![]() . La soluzione venne
diluita a
. La soluzione venne
diluita a ![]() con acqua, un elettrodo ad
con acqua, un elettrodo ad ![]() venne
immerso in essa alla temperatura di
venne
immerso in essa alla temperatura di ![]() e la differenza di
potenziale tra questo elettrodo e un elettrodo standard ad idrogeno fu
trovata essere pari a
e la differenza di
potenziale tra questo elettrodo e un elettrodo standard ad idrogeno fu
trovata essere pari a ![]() . Qual'era la percentuale in massa
di
. Qual'era la percentuale in massa
di ![]() nel campione?
nel campione?
(
![]() )
)
Dati:

Altri simboli:
|
|
la percentuale in massa di |
| massa di |
|
| numero di moli di |
|
| massa molare di |
|
| concentrazione di |
|
| costante di Faraday: |
|
| costante dei gas:
|
|
| potenziale elettrodico dell'elettrodo standard a idrogeno: |
Applicando le definizioni di percentuale...
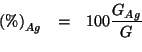
...massa molare...
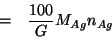
...e concentrazione...
si puo' esprimere la percentuale cercata in funzione di quantita' note
e della concentrazione di ![]() nella soluzione.
nella soluzione.
A questo punto, per trovare
![]() si sfrutta il dato
della differenza di potenziale; infatti, il potenziale elettrodico
dell'elettrodo ad argento e' legato alla concentrazione di ioni
argento dalla relazione di Nernst mentre il potenziale elettrodico
dell'elettrodo standard ad idrogeno e' ovviamente nullo per
convenzione. Tenendo presente che la semireazione relativa
all'elettrodo ad argento e':
si sfrutta il dato
della differenza di potenziale; infatti, il potenziale elettrodico
dell'elettrodo ad argento e' legato alla concentrazione di ioni
argento dalla relazione di Nernst mentre il potenziale elettrodico
dell'elettrodo standard ad idrogeno e' ovviamente nullo per
convenzione. Tenendo presente che la semireazione relativa
all'elettrodo ad argento e':
si ha:
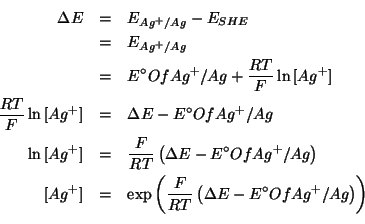
Sostituendo nell'equazione ![]() si ottiene:
si ottiene:
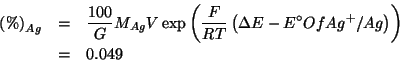
Si hanno a disposizione ![]() di acido propionico
(
di acido propionico
(![]() )
) ![]() .
.
(
![]() )
)
Dati:

Altri simboli:
| volume della soluzione di |
|
| numero di moli di |
|
|
|
volume della soluzione di |
|
|
numero di moli di |
| volume di |
|
|
|
|
|
|
|
|
|
concentrazione di ioni idrogeno prima dell'aggiunta di |
|
|
concentrazione di ioni idrogeno dopo l'aggiunta di |
|
|
numero di moli di |
Per ciascuno dei tre quesiti conviene considerare una situazione
iniziale corrispondente all'acido propionico indissociato in presenza
del componente aggiunto (![]() ,
, ![]() o
o ![]() ):
abbiamo la garanzia che lo stato di equilibrio finale raggiunto dal
sistema e' sempre lo stesso. Inoltre, gli elettroliti forti, cioe'
):
abbiamo la garanzia che lo stato di equilibrio finale raggiunto dal
sistema e' sempre lo stesso. Inoltre, gli elettroliti forti, cioe'
![]() e
e ![]() , si possono considerare completamente
dissociati.
, si possono considerare completamente
dissociati.
Fatte queste premesse, i tre casi si affrontano descrivendo l'equilibrio di ionizzazione dell'acido propionico a partire dalle condizioni iniziali specificate.
Il sistema viene descritto come segue:

Osserviamo che l'incognita da trovare e'
![]() ,
cioe', in pratica, la concentrazione iniziale di acido cloridrico,
visto che esso e' completamente dissociato. Come al solito, possiamo
trascurare la concentrazione di ioni idrogeno provenienti
dall'autoionizzazione dell'acqua. La concentrazione di equilibrio
degli ioni idrogeno,
,
cioe', in pratica, la concentrazione iniziale di acido cloridrico,
visto che esso e' completamente dissociato. Come al solito, possiamo
trascurare la concentrazione di ioni idrogeno provenienti
dall'autoionizzazione dell'acqua. La concentrazione di equilibrio
degli ioni idrogeno,
![]() , e' data, essendo ricavabile
immediatamente dal
, e' data, essendo ricavabile
immediatamente dal ![]() che si deve realizzare.
che si deve realizzare.
A questo punto si scrive la legge dell'azione di massa e si risolve
rispetto all'incognita
![]() :
:

Il risultato ottenuto merita una considerazione. Infatti, la
concentrazione di ![]() da aggiungere risulta uguale a
quella che si dovrebbe avere in acqua pura per ottenere il
da aggiungere risulta uguale a
quella che si dovrebbe avere in acqua pura per ottenere il ![]() richiesto. Cio' e' ragionevole, in quanto l'acido propionico e' debole
e quindi, in presenza di un acido forte come
richiesto. Cio' e' ragionevole, in quanto l'acido propionico e' debole
e quindi, in presenza di un acido forte come ![]() , la sua
dissociazione sara' praticamente trascurabile. In altre parole, tutto
funziona come se l'acido propionico non ci fosse.
, la sua
dissociazione sara' praticamente trascurabile. In altre parole, tutto
funziona come se l'acido propionico non ci fosse.
Rimane da trovare il volume della soluzione di ![]() che, aggiunto
alla soluzione di acido propionico di partenza, realizza la
concentrazione iniziale di ioni idrogeno trovata piu' sopra. A tale
scopo e' sufficiente applicare la definizione di concentrazione:
che, aggiunto
alla soluzione di acido propionico di partenza, realizza la
concentrazione iniziale di ioni idrogeno trovata piu' sopra. A tale
scopo e' sufficiente applicare la definizione di concentrazione:
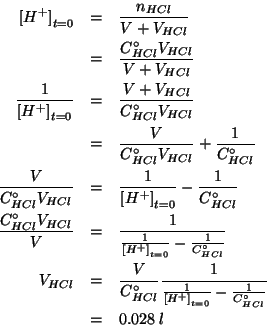
Si considera sempre l'equlibrio di ionizzazione dell'acido propionico, con le nuove condizioni iniziali:
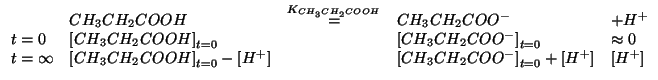
Come nel caso precedente, l'incognita e'
![]() , ovvero la concentrazione iniziale
di
, ovvero la concentrazione iniziale
di ![]() , visto che si tratta di un elettrolita forte. Trascurando in prima approssimazione l'autoionizzazione dell'acqua, la concentrazione
iniziale di ioni idrogeno e' nulla; quella finale si ricava
immediatamente dal
, visto che si tratta di un elettrolita forte. Trascurando in prima approssimazione l'autoionizzazione dell'acqua, la concentrazione
iniziale di ioni idrogeno e' nulla; quella finale si ricava
immediatamente dal ![]() che si deve realizzare.
che si deve realizzare.
Come di consueto, scriviamo la legge dell'azione di massa e risolviamo rispetto all'incognita:

Come previsto, il valore trovato e' minore di ![]() .
.
Come per il caso precedente, dobbiamo ora trovare il volume della
soluzione di ![]() che, aggiunto alla soluzione di acido
propionico di partenza, realizza la concentrazione iniziale di ioni
che, aggiunto alla soluzione di acido
propionico di partenza, realizza la concentrazione iniziale di ioni
![]() trovata piu' sopra. Il calcolo e' evidentemente
identico a quello visto al punto precedente:
trovata piu' sopra. Il calcolo e' evidentemente
identico a quello visto al punto precedente:

Cominciamo con lo scrivere matematicamente cio' che il quesito richiede:
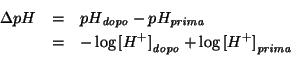
Le due concentrazioni di ioni idrogeno si trovano considerando sempre l'equilibrio di ionizzazione dell'acido, con le opportune condizioni iniziali:
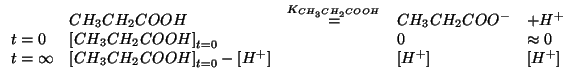
La legge dell'azione di massa diventa:
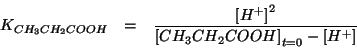
Si possono fare a questo punto le usuali considerazioni semplificative: siccome la costante dell'acido propionico e' piccola, esso si dissociera' poco e quindi la concentrazione di ioni idrogeno all'equilibrio puo' essere trascurata rispetto alla concentrazione iniziale di acido.
Sinteticamente:
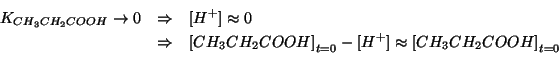
Quindi:
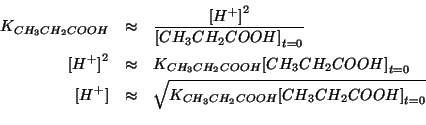
Questo e' il ben noto risultato per la ionizzazione di un acido debole. Prima della diluizione, la concentrazione iniziale dell'acido e' quella data dal problema e quindi:
Dopo l'aggiunta dell'acqua, la concentrazione di acido a ![]() sara'
minore a causa della diluzione:
sara'
minore a causa della diluzione:
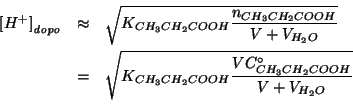
Non resta che sostituire piu' sopra e risolvere rispetto a
![]() :
:

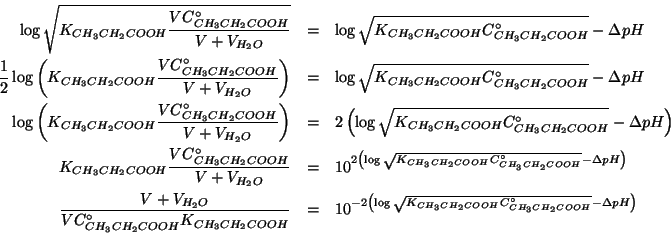
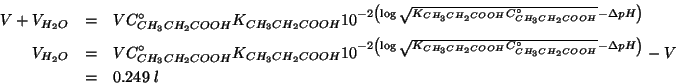
La massa atomica del bismuto deve essere determinata convertendo il
composto
![]() in
in ![]() . Se da
. Se da
![]() di
di
![]() si ottengono
si ottengono ![]() di
di ![]() , qual'e' la massa atomica del bismuto?
, qual'e' la massa atomica del bismuto?
Dati:

Altri simboli:
| massa molare di |
|
| massa molare di |
|
| massa molare di |
|
| massa molare di |
|
|
|
massa molare di |
|
|
massa molare di |
| numero di moli di |
|
|
|
numero di moli di |
| numero di moli di |
Cominciamo con l'osservare che il numero di moli di bismuto contenuto
nei due campioni deve essere lo stesso, per un ovvio bilancio di
massa:
ovvero, dalla formula dei composti: