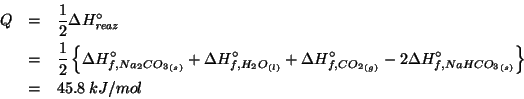25 settembre 2000
Prova scritta di Chimica I

Esercizio 1

Calcolare il $pH$ di una soluzione di cinnamato di sodio $C_9H_7O_2Na$, sale di un acido debole monobasico, dai seguenti dati.

1. la soluzione in questione, avente densita' $1.06\;g/ml$, presenta un abbassamento del punto di fusione di $0.208\;C$ (la costante crioscopica dell'acqua e' $k_{cr}=1.86\;K\;kg/mol$)
2. una soluzione $0.05\;mol/l$ di acido cinnamico ha un $pH$ pari a $2.87$

SVOLGIMENTO

Dati:

$\begin{array}{rl} \Delta{}T&0.208\;K\\ d&1.06\;g/ml\\ k_{cr}&1.86\;K\;kg/mol\\ C^\circ_{HA}&0.05\;mol/l\\ pH_{HA}&2.87 \end{array}$

Altri simboli:

$m$	molalita' della soluzione di cinnamato sodico
$n^\circ_{NaA}$	numero di moli di cinnamato sodico
$V$	volume della soluzione di cinnamato sodico in $l$
$G$	massa della soluzione di cinnamato sodico in $kg$
$G_{H_2O}$	massa d'acqua contenuta nella soluzione di cinnamato sodico in $kg$
$G_{NaA}$	massa di sale contenuto nella soluzione di cinnamato sodico in $kg$
$g_{NaA}$	massa di sale contenuto nella soluzione di cinnamato sodico in $g$
$C^\circ_{NaA}$	concentrazione molare di cinnamato sodico
$M_{NaA}$	massa molare del cinnamato sodico: $170.14\;g/mol$
$K_{i}$	costante di idrolisi dello ione cinnamato
$K_{HA}$	costante di ionizzazione dell'acido cinnamico
$K_{W}$	costante di autoionizzazione dell'acqua: $1\times10^{-14}$

Siccome il cinnamato di sodio (che per brevita' indicheremo con $NaA$) e' il sale di un acido debole monoprotico, il $pH$ di una sua soluzione sara' basico a causa dell'idrolisi dell'anione $A^-$:

$$\begin{eqnarray*} A^-+H_2O&=&AH+OH^- \end{eqnarray*}$$

Per analizzare l'equilibrio appena scritto dobbiamo conoscere la concentrazione iniziale di $A^-$ (che coincide con quella di $NaA$, poiche' quest'ultimo e' un elettrolita forte) e la costante di equilibrio. E' facile verificare che la costante di equilibrio e' data da:

$$\begin{eqnarray*} K_i&=&\frac{K_W}{K_{HA}} \end{eqnarray*}$$

per cui dobbiamo trovare $K_{HA}$.

La concentrazione iniziale di sale si ricava dai dati relativi all'abbassamento crioscopico. A questo proposito va osservato che il cinnamato sodico e' un elettrolita forte e quindi si dissocia completamente secondo:

$$\begin{eqnarray*} NaA&=&Na^++A^- \end{eqnarray*}$$

Questo significa che la molalita' da usare nell'espressione dell'abbassamento crioscopico (la cosiddetta ``molalita' colligativa'') e' doppia rispetto alla molalita' del sale. In termini matematici:

$$\begin{eqnarray*} \Delta{}T&=&k_{cr}2m\\ m&=&\frac{\Delta{}T}{2k_{cr}} \end{eqnarray*}$$

Ora si deve trasformare la molalita' $m$ nella molarita' iniziale del sale $C^\circ_{NaA}$.

Per definizione:

$$\begin{eqnarray*} C^\circ_{NaA}&=&\frac{n^\circ_{NaA}}{V} \end{eqnarray*}$$

Il volume della soluzione si puo' esprimere in funzione della massa e della densita':

$$\begin{eqnarray*} &=&\frac{n^\circ_{NaA}}{\frac{G}{d}}\\ &=&\frac{n^\circ_{NaA}}{\frac{G_{H_2O}+G_{NaA}}{d}} \end{eqnarray*}$$

Dividendo numeratore e denominatore per $n^\circ_{NaA}$:

$$\begin{eqnarray*} &=&\frac{1}{\frac{\frac{G_{H_2O}}{n^\circ_{NaA}}+\frac{G_{NaA}}{n^\circ_{NaA}}}{d}} \end{eqnarray*}$$

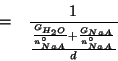
Il primo addendo al denominatore e' proprio l'inverso della molalita'. Il secondo addendo e' ``quasi'' la massa molare del sale. Il ``quasi'' e' dovuto al fatto che $G_{NaA}$ e' la massa di sale in $kg$, mentre la massa molare che siamo abituati a usare e' espressa in $g/mol$ e quindi richiede la massa in $g$. Chiaramente, vale: $G_{NaA}=10^{-3}g_{NaA}$, e quindi:

$$\begin{eqnarray*} &=&\frac{1}{\frac{\frac{1}{m}+\frac{10^{-3}g_{NaA}}{n^\circ_{N... ...{2k_{cr}}}+10^{-3}M_{NaA}}{d}}\\ &=&5.87\times10^{-2}\;mol/l\\ \end{eqnarray*}$$

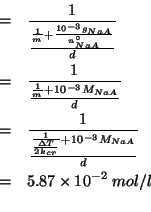
Il primo requisito (la concentrazione iniziale del sale) per il trattamento dell'equilibrio di idrolisi e' stato cosi' ottenuto.

L'altra cosa che ci serve e' la costante di ionizzazione dell'acido cinnamico $HA$. Per trovarla, utilizziamo la seconda informazione che ci viene data, e cioe' quella relativa al $pH$ di una soluzione dell'acido di concentrazione iniziale nota.

Impostiamo il consueto trattamento dell'equilibrio di ionizzazione:

$$\begin{array}{lllll} &HA &\stackrel{K_{HA}}{=}& A^-&+H^+\\ ... ...\left[H^+\right]&&\left[H^+\right]&\left[H^+\right] \end{array}$$

La legge dell'azione di massa e':

$$\begin{eqnarray*} K_{HA}&=&\frac{\left[H^+\right]^2}{\left[HA\right]_{t=0}-\left[H^+\right]} \end{eqnarray*}$$

Osservate che la concentrazione di equilibrio degli ioni idrogeno e' nota, essendo legata al $pH$ dato nel testo.

Quindi:

$$\begin{eqnarray*} K_{HA}&=&\frac{10^{-2pH_{HA}}}{C^\circ_{HA}-10^{-pH_{HA}}}\\ &=&3.74\times10^{-5} \end{eqnarray*}$$

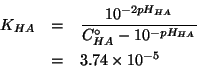
Abbiamo ora tutto cio' che ci serve per trattare l'equilibrio di idrolisi che costituisce l'obiettivo dell'esercizio.

$$\begin{array}{llllll} &A^-&+H_2O&\stackrel{K_{i}}{=}& AH&+OH... ...t[OH^-\right]&&&\left[OH^-\right]&\left[OH^-\right] \end{array}$$

Scriviamo la legge dell'azione di massa, esprimendo la costante di equilibrio in termini della costante di ionizzazione trovata prima:

$$\begin{eqnarray*} \frac{K_W}{K_{HA}}&=&\frac{\left[OH^-\right]^2}{\left[A^-\righ... ...=&\frac{\left[OH^-\right]^2}{C^\circ_{NaA}-\left[OH^-\right]}\\ \end{eqnarray*}$$

L'equazione puo'essere risolta cosi' com'e'. Tuttavia, possiamo osservare che $K_W/K_{HA}$ e' dell'ordine di $10^{-9}$. Cio' significa che in prima approssimazione si puo' trascurare la frazione di cinnamato che idrolizza.

In termini matematici:

$$\begin{eqnarray*} \frac{K_W}{K_{HA}}\rightarrow0&\Rightarrow&\left[OH^-\right]\l... ...htarrow&C^\circ_{NaA}-\left[OH^-\right]\approx{}C^\circ_{NaA}\\ \end{eqnarray*}$$

Quindi:

$$\begin{eqnarray*} \frac{K_W}{K_{HA}}&\approx&\frac{\left[OH^-\right]^2}{C^\circ_{NaA}}\\ \end{eqnarray*}$$

da cui:

$$\begin{eqnarray*} \left[OH^-\right]^2&\approx&C^\circ_{NaA}\frac{K_W}{K_{HA}}\\ ... ...c{K_W}{\sqrt{C^\circ_{NaA}\frac{K_W}{K_{HA}}}}\right)\\ &=&8.60 \end{eqnarray*}$$

Esercizio 2

Utilizzando i formalismi appresi nel corso (formule di Lewis, teoria VSEPR, teoria del legame di valenza) descrivere il legame e la geometria nelle seguenti meolecole o ioni:

1. $ICl_4^-$
2. $PCl_4^+$
3. $CS_2$
4. $ClO_2^-$

SVOLGIMENTO

1. $ICl_4^-$

   Cominciamo a scrivere la formula di Lewis.

   Elettroni di valenza
   $I$	$7$
   $Cl$	$4\times7$
   carica	1
   totale	$36$

   L'unica struttura di Lewis ragionevole e':

   
   

   $$\left[ \begin{xy} <1em,0em>: c*+{I};p=''center'', p+/l3em/*... ...r{\vert}, p+/dl0.1em/**\dir{}?<*\dir{\vert}, \end{xy}\right]^-$$
   
   

   
   
   
   

   Determinazione della geometria con la teoria VSEPR
   coppie strutturali	6
   geometria delle coppie strutturali	ottaedrica
   modello	$\begin{xy} <1em,0em>: c*+{I};p=''I''; p+/u3em/**\dir{-},c=''Cl'', p+/d3em/**\... ..., ''vertex'';''I''**\dir{-}?>;p+/u0.5em/**\dir{-};''vertex''**\dir{-}; \end{xy}$
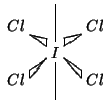   coppie di non legame	2
   geometria molecolare	planare quadrata

   Osserviamo che, siccome le coppie solitarie sono ``piu' repulsive'' delle coppie di legame, le due coppie di non legame si sistemano da parti opposte del piano formato dagli atomi di $Cl$.

   
   
   
   Dalla geometria delle coppie strutturali ricavata si deduce che l'ibridazione dell'atomo centrale deve essere di tipo $sp^3d^2$. Nella formula di Lewis l'atomo di $I$ possiede $8$ elettroni di valenza mentre ciascun atomo di $Cl$ ne possiede $7$. Ne risulta lo schema di sovrapposizione seguente.

   
   
   

2. $PCl_4^+$

   Formula di Lewis.

   Elettroni di valenza
   $P$	$5$
   $Cl$	$4\times7$
   carica	-1
   totale	$32$

   Possibili formule di Lewis:

   
   

   $$\begin{array}{cc} \left[ \begin{xy} <1em,0em>: c*+{P}; p+/l... ...*\dir{\vert}, \end{xy}\right]^+ \\ &\\ (A)&(B)\\ \end{array}$$
   
   

   La struttura $(B)$ (e le tre strutture di risonanza ad essa equivalenti, non mostrate per brevita') e' meno stabile della struttura $(A)$ poiche' prevede una carica atomica formale pari a $+1$ sull'atomo di $Cl$ legato con doppio legame.

   
   
   
   

   Determinazione della geometria con la teoria VSEPR
   coppie strutturali	4
   geometria delle coppie strutturali	tetraedrica
   modello	$\begin{xy} <1em,0em>: c*+{P};p=''P''; p+/u3em/*+{Cl}**\dir{-},c=''ClUp'', p+/... ...c=''vertex''; ''P''**\dir{-}?>;p+/u0.5em/**\dir{-};''vertex''**\dir{-} \end{xy}$
   coppie di non legame	0
   geometria molecolare	tetraedrica

   
   
   
   Dalla geometria delle coppie strutturali ricavata si deduce che l'ibridazione dell'atomo centrale deve essere di tipo $sp^3$. Nella formula di Lewis piu' stabile (la $(A)$) l'atomo di $P$ possiede $4$ elettroni di valenza mentre ciascun atomo di $Cl$ ne possiede $7$. Ne risulta lo schema di sovrapposizione seguente.

   
   
   

3. $CS_2$

   Formula di Lewis.

   Elettroni di valenza
   $C$	$4$
   $S$	$2\times6$
   totale	$16$

   Possibili formule di Lewis:

   
   

   $$\begin{array}{cc} \begin{xy} c*+{C}; p+/l3em/*+{S}**\dir{=},... ...**\dir{}?<*\dir{\vert}, \end{xy}\\ &\\ (A)&(B)\\ \end{array}$$
   
   

   La struttura $(B)$ (e la struttura di risonanza ad essa equivalente, non mostrata per brevita') e' meno stabile della struttura $(A)$ poiche', diversamente da questa, prevede cariche atomiche formali non nulle ($-1$ e $+1$) sugli atomi di $S$.

   
   
   
   

   Determinazione della geometria con la teoria VSEPR
   coppie strutturali	2
   geometria delle coppie strutturali	lineare
   modello	$\begin{xy} c*+{C}; p+/l3em/*+{S}**\dir{-}, p+/r3em/*+{S}**\dir{-}, \end{xy}$
   coppie di non legame	0
   geometria molecolare	lineare

   
   
   
   Dalla geometria delle coppie strutturali ricavata si deduce che l'ibridazione dell'atomo centrale deve essere di tipo $sp$. Nella formula di Lewis piu' stabile (la $(A)$) l'atomo di $C$ possiede $4$ elettroni di valenza mentre ciascun atomo di $S$ ne possiede $6$. Inoltre, si vede che l'atomo di carbonio forma due legami di tipo $\sigma$ e due legami di tipo $\pi$. Ne risulta uno schema di sovrapposizione identico a quello di $CO_2$.

   
   
   

4. $ClO_2^-$

   Formula di Lewis.

   Elettroni di valenza
   $Cl$	$7$
   $O$	$2\times6$
   carica	1
   totale	$20$

   Possibili formule di Lewis:

   
   

   $$\begin{array}{ccc} \left[ \begin{xy} c*+{Cl}; p+/u0.1em/**\d... ...{\vert}, \end{xy}\right]^- \\ &&\\ (A)&(B)&(C)\\ \end{array}$$
   
   

   Le strutture $(B)$ e $(C)$ (fra loro identiche) sono piu' stabili della struttura $(A)$, poiche' le cariche atomiche formali sono minori (osservate che il $Cl$ puo' avere valenza espansa).

   
   
   
   

   Determinazione della geometria con la teoria VSEPR
   coppie strutturali	4
   geometria delle coppie strutturali	tetraedrica
   modello	$\begin{xy} <1em,0em>: c*+{Cl};p=''Cl''; p+/u3em/*+{O}**\dir{-},c=''OUp'', p+/... ...=''vertex''; ''Cl''**\dir{-}?>;p+/u0.5em/**\dir{-};''vertex''**\dir{-} \end{xy}$
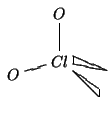   coppie di non legame	2
   geometria molecolare	angolata

   
   
   
   Dalla geometria delle coppie strutturali ricavata si deduce che l'ibridazione dell'atomo centrale deve essere di tipo $sp^3$. Nella formula di Lewis piu' stabile (la $(B)$ o la $(C)$, e' indifferente) l'atomo di $Cl$ possiede $7$ elettroni di valenza; l'atomo di $O$ legato con doppio legame ne possiede $6$ mentre l'atomo di $O$ legato con legame singolo ne possiede $7$. Ne risulta uno schema di sovrapposizione come quello mostrato qui di seguito.

   
   
   

Esercizio 3

Calcolare il calore da fornire ad una mole di idrogeno carbonato di sodio per far avvenire la decomposizione seguente in condizioni standard:

$$\begin{eqnarray*} 2\Solid{NaHCO_3}&=&\Solid{Na_2CO_3}+\Liquid{H_2O}+\Gaseous{CO_2} \end{eqnarray*}$$

I valori dell'entalpia molare standard di formazione per $\Solid{NaHCO_3}$ $\Solid{Na_2CO_3}$ $\Liquid{H_2O}$ e $\Gaseous{CO_2}$ sono, rispettivamente, $-950.8\;kJ/mol$, $-1130.7\;kJ/mol$, $-285.8\;kJ/mol$ e $-393.5\;kJ/mol$.

SVOLGIMENTO

Dati:

$\begin{array}{rl} \DeltaHZeroFOf{\Solid{NaHCO_3}}&-950.8\;kJ/mol\\ \DeltaHZer... ...&-285.8\;kJ/mol\\ \DeltaHZeroFOf{\Gaseous{CO_2}}&-393.5\;kJ/mol\\ \end{array}$

Altri simboli:

$\Delta{}H^\circ_{\mathit{reaz}}$

variazione di entalpia per la reazione in condizioni standard

Il calore richiesto coincide con la variazione di entalpia per la reazione nelle condizioni date. Quest'ultima, a sua volta, si ricava dalle entalpie di formazione dei reagenti e prodotti come visto durante il corso.

Da notare che il problema richiede il calore da fornire ad una mole di $NaHCO_3$: cio' significa che la variazione di entalpia per la reazione va divisa per 2, poiche' la reazione coinvolge $2\;mol$ di $NaHCO_3$.

Quindi:

$$\begin{eqnarray*} Q&=&\frac{1}{2}\Delta{}H^\circ_{\mathit{reaz}}\\ &=&\frac{1}{... ...eous{CO_2}}-2\DeltaHZeroFOf{\Solid{NaHCO_3}}}\\ &=&45.8\;kJ/mol \end{eqnarray*}$$