Sapendo che la temperatura di congelamento del cicloesano e'
![]() e che la soluzione ottenuta sciogliendo
e che la soluzione ottenuta sciogliendo ![]() di un
composto organico in
di un
composto organico in ![]() di cicloesano congela a
di cicloesano congela a ![]() ,
calcolare la massa molare del composto.
,
calcolare la massa molare del composto.
La costante crioscopica del cicloesano e'
![]() .
.
Dati:

Altri simboli:
| molalita' del composto | |
| numero di moli del composto | |
| la massa molare cercata |
Cominciamo a scrivere la equazione che regola l'abbassamento
crioscopico:
Ora dobbiamo esprimere la molalita' in funzione della massa molare che stiamo cercando. A questo scopo utilizziamo la definizione di molalita':
Il numero di moli del composto si puo' esprimere in funzione della sua massa (nota) e della sua massa molare:
A questo punto non resta che risolvere per ![]() :
:
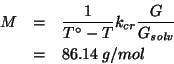
Scrivere la reazione fra le coppie redox
![]() (
(
![]() ) e
) e ![]() (
(
![]() ) nel verso in cui avviene in
condizioni standard a
) nel verso in cui avviene in
condizioni standard a ![]() . Scrivere l'espressione della
costante di equilibrio e calcolarne il valore. Se le concentrazioni
degli ioni ferrico, ferroso e argento sono rispettivamente
. Scrivere l'espressione della
costante di equilibrio e calcolarne il valore. Se le concentrazioni
degli ioni ferrico, ferroso e argento sono rispettivamente
![]() ,
, ![]() e
e ![]() il verso della
reazione e' ancora quello in condizioni standard? Calcolare le
concentrazioni dei tre ioni all'equilibrio.
il verso della
reazione e' ancora quello in condizioni standard? Calcolare le
concentrazioni dei tre ioni all'equilibrio.
Dati:
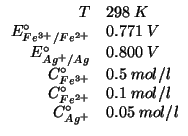
Altri simboli:
| costante di equilibrio per la reazione | |
| costante dei gas:
|
|
| costante di Faraday: |
Siccome il potenziale standard esprime la tendenza alla riduzione in condizioni standard per una data coppia redox, dal fatto che:
si deduce che, in condizioni standard, lo ione argento tende a ossidare lo ione ferro (II) a ione ferro (III), riducendosi ad argento metallico. In altri termini, il verso spontaneo della reazione redox globale in condizioni standard e':
Come per tutte le reazioni, l'espressione della costante di equilibrio e':
Il valore di ![]() si trova ricordando che la costante di equilibrio
di una reazione redox e' legata alla differenza dei potenziali
elettrodici standard tramite:
si trova ricordando che la costante di equilibrio
di una reazione redox e' legata alla differenza dei potenziali
elettrodici standard tramite:
Nel caso presente, la relazione diventa:
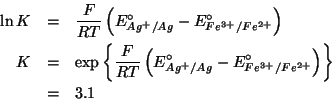
Consideriamo ora il caso in cui il sistema non e' in condizioni standard. In questo caso il criterio di spontaneita' deve utilizzare i potenziali elettrodici non standard, che si ottengono con l'equazione di Nernst.
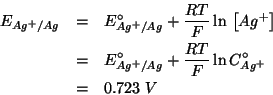
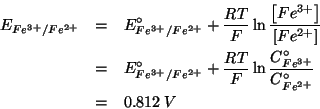
Come vediamo, quindi, in questo caso si ha:
e cio' significa che il verso spontaneo della reazione sara':
cioe' opposto a quello in condizioni standard.
Resta il calcolo delle concentrazioni di equilibrio. Impostiamo la
tabella usuale prendendo la concentrazione di equilibrio dello ione
![]() come incognita. Basandoci sulla stechiometria della
reazione e sul fatto che conosciamo il verso in cui si evolve, si ha:
come incognita. Basandoci sulla stechiometria della
reazione e sul fatto che conosciamo il verso in cui si evolve, si ha:
![\begin{displaymath}
\begin{array}{llllll}
&Ag&+Fe^{3+}&=&Ag^+&+Fe^{2+}\\
t=0&&\...
...Fe^{2+}\right]_{t=0}\right)&\left[Fe^{2+}\right]\\
\end{array}\end{displaymath}](img38.gif)
La legge dell'azione di massa e':
(Notate che la costante di equilibrio per la reazione cosi' come l'abbiamo scritta piu' sopra e' l'inverso della costante di equilibrio che abbiamo calcolato all'inizio, perche' il verso della reazione e' invertito)
Proseguendo nella soluzione:
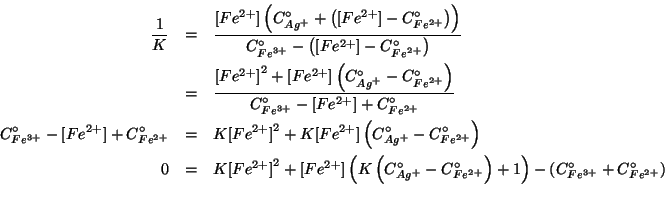
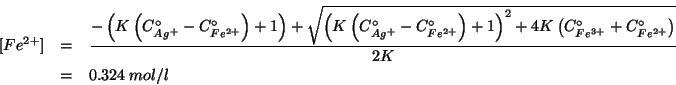
Le altre due concentrazioni si ricavano dalle relazioni che abbiamo scritto nella tabella relativa all'equilibrio.
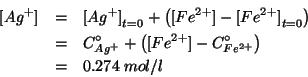
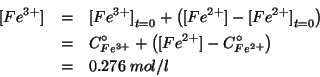
Un composto di formula ![]() subisce decomposizione termica
secondo la seguente equazione:
subisce decomposizione termica
secondo la seguente equazione:
Un eccesso di ![]() viene riscaldato da
viene riscaldato da ![]() a
a ![]() in
un recipiente chiuso contenente
in
un recipiente chiuso contenente ![]() gassoso. Le pressioni iniziale
(a
gassoso. Le pressioni iniziale
(a ![]() ) e finale (a
) e finale (a ![]() ) sono rispettivamente
) sono rispettivamente
![]() e
e
![]() . Calcolare la costante di
equilibrio
. Calcolare la costante di
equilibrio ![]() della reazione a
della reazione a ![]() .
.
Dati:
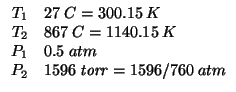
Altri simboli:
| numero di moli iniziale di |
|
|
|
numero di moli di |
| numero di moli di |
|
| pressione parziale di |
|
| pressione parziale di |
|
| volume (incognito, ma costante) del recipiente in |
|
| costante dei gas:
|
|
| costante di equilibrio della reazione da determinare |
Prima di tutto scriviamo la definizione della costante ![]() per
capire cosa ci serve:
per
capire cosa ci serve:
Cioe': dobbiamo trovare le due pressioni parziali all'equilibrio.
Una prima relazione che lega le pressioni parziali di equilibrio e' ovviamente questa:
poiche' all'equilibrio gli unici componenti gassosi sono ![]() e
e
![]() .
.
Ci occorre ora una seconda relazione (indipendente) che leghi le due
pressioni parziali. Tale relazione si ottiene da un bilancio di
massa; le moli di ![]() all'equilibrio devono essere evidentemente
date dalla somma delle moli inizialmente presenti piu' quelle che si
sono formate dalla reazione:
all'equilibrio devono essere evidentemente
date dalla somma delle moli inizialmente presenti piu' quelle che si
sono formate dalla reazione:
Dalla stechiometria della reazione, osserviamo che le moli di ![]() formate dalla reazione devono essere numericamente uguali alle moli di
formate dalla reazione devono essere numericamente uguali alle moli di
![]() formate; ma siccome
formate; ma siccome ![]() era inizialmente assente, le
moli di
era inizialmente assente, le
moli di ![]() formate coincidono con le moli di
formate coincidono con le moli di ![]() all'equilibrio. Quindi:
all'equilibrio. Quindi:
Ricordate che stiamo cercando una relazione tra le pressioni parziali; allora possiamo esprimere i numeri di moli con la legge dei gas ideali. Cosi' facendo introduciamo il volume incognito, ma si vede facilmente che esso compare in ogni termine e quindi si puo' semplificare.
Allora:
Osservate che abbiamo espresso ![]() sfruttando i dati alla
temperatura
sfruttando i dati alla
temperatura ![]() poiche' in quelle condizioni
poiche' in quelle condizioni ![]() era l'unico
componente gassoso presente.
era l'unico
componente gassoso presente.
Semplifichiamo e riarrangiamo:
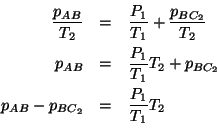
e questa e' la seconda relazione che ci serviva.
Riscriviamo le due relazioni trovate per chiarezza:
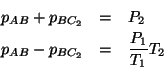
Questo sistema lineare fornisce le pressioni parziali che possono poi
essere inserite nell'espressione per ![]() .
.
Sommando le due equazioni membro a membro si ha:
![\begin{eqnarray*}
2p_{AB}&=&P_2+\frac{P_1}{T_1}T_2\\
p_{AB}&=&\frac{1}{2}\left[P_2+\frac{P_1}{T_1}T_2\right]\\
\end{eqnarray*}](img71.gif)
e, sostituendo l'espressione appena trovata per ![]() nella prima
relazione scritta sopra:
nella prima
relazione scritta sopra:
![\begin{eqnarray*}
p_{BC_2}&=&P_2-p_{AB}\\
&=&P_2-\frac{1}{2}\left[P_2+\frac{P_1}{T_1}T_2\right]\\
\end{eqnarray*}](img72.gif)
Non resta che sostituire le pressioni parziali cosi' ottenute nella
definizione di ![]() e fare i calcoli numerici:
e fare i calcoli numerici:
![\begin{eqnarray*}
K_P&=&p_{AB}p_{BC_2}\\
&=&\left(\frac{1}{2}\left[P_2+\frac{P_...
...ac{1}{2}\left[P_2+\frac{P_1}{T_1}T_2\right]\right)\\
&=&0.20\\
\end{eqnarray*}](img73.gif)