![]() di un composto organico contenente carbonio, idrogeno e
ossigeno vengono bruciati con ossigeno in eccesso. Dalla combustione
si ottengono
di un composto organico contenente carbonio, idrogeno e
ossigeno vengono bruciati con ossigeno in eccesso. Dalla combustione
si ottengono ![]() di
di ![]() e
e ![]() di
di
![]() . Calcolare la formula minima del composto.
. Calcolare la formula minima del composto.
Dati:
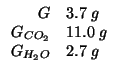
Altri simboli:
| numero di moli del composto contenuto in |
|
| massa molare di |
|
| massa molare di |
|
| massa di carbonio in grammi contenuta in |
|
| massa di idrogeno in grammi contenuta in |
|
| massa di ossigeno in grammi contenuta in |
|
| massa molare di |
|
| massa molare di |
|
| massa molare di |
Per cominciare, assumiamo che la formula minima cercata sia:
![]() . Se indichiamo con
. Se indichiamo con ![]() il numero di moli del composto
organico contenuti nei
il numero di moli del composto
organico contenuti nei ![]() dati dal problema, allora la
reazione di combustione puo' essere descritta dalla seguente
equazione:
dati dal problema, allora la
reazione di combustione puo' essere descritta dalla seguente
equazione:
Il numero ![]() di moli di ossigeno richiesto dalla stechiometria non
ha importanza, in quanto sappiamo che l'ossigeno e' stato impiegato
in eccesso. La cosa importante e' che dalle
di moli di ossigeno richiesto dalla stechiometria non
ha importanza, in quanto sappiamo che l'ossigeno e' stato impiegato
in eccesso. La cosa importante e' che dalle ![]() moli di composto
organico si devono essere formate
moli di composto
organico si devono essere formate ![]() moli di
moli di ![]() e
e
![]() moli di
moli di ![]() . Questi numeri di moli possono
essere messi facilmente in relazione con le corrispondenti quantita'
in grammi:
. Questi numeri di moli possono
essere messi facilmente in relazione con le corrispondenti quantita'
in grammi:
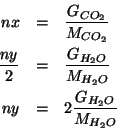
Per le moli di ossigeno contenute nelle ![]() moli di composto
possiamo scrivere una relazione analoga:
moli di composto
possiamo scrivere una relazione analoga:
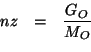
La massa di ossigeno puo' essere espressa per differenza, visto che il
composto contiene solo ![]() ,
, ![]() e
e ![]() :
:
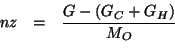
Ora esprimiamo le masse in grammi di ![]() e
e ![]() in funzione dei
corrispondenti numeri di moli e delle masse molari:
in funzione dei
corrispondenti numeri di moli e delle masse molari:
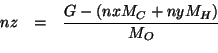
Sostituiamo le espressioni prima trovate per ![]() e
e ![]() :
:
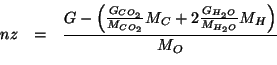
A questo punto abbiamo:
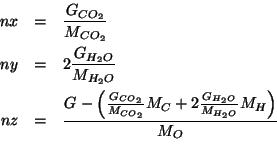
Nelle tre espressioni compare ![]() , che non conosciamo. Tuttavia,
facendo il rapporto membro a membro, il termine
, che non conosciamo. Tuttavia,
facendo il rapporto membro a membro, il termine ![]() si semplifica e
otteniamo:
si semplifica e
otteniamo:
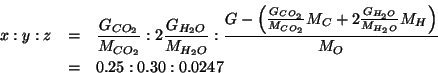
Infine, i rapporti ottenuti possono essere trasformati in numeri interi dividendo ciascun valore per il piu' piccolo dei tre:
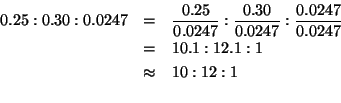
Quindi, la formula minima e': ![]() .
.
Il potenziale standard della coppia ione iodato/ione ioduro in
ambiente basico e' ![]() ; quello della coppia ione
permanganato/diossido di manganese nello stesso ambiente e'
; quello della coppia ione
permanganato/diossido di manganese nello stesso ambiente e'
![]() .
.
Stabilire se, in condizioni standard, lo ione iodato e' capace di ossidare il diossido di manganese o se , viceversa, lo ione permanganato ossida lo ione ioduro.
Scrivere e bilanciare la reazione nella direzione in cui avviene (il diossido di manganese e' un solido insolubile nell'ambiente di reazione).
Dati:
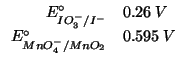
Ricordando che il potenziale di riduzione indica la tendenza di una semireazione a procedere nel verso della riduzione, si deduce immediatamente che il processo termodinamicamente favorito e' l'ossidazione dello ione ioduro da parte dello ione permanganato, dal momento che si ha:
Per il bilanciamento si ha, applicando il metodo illustrato durante il corso:
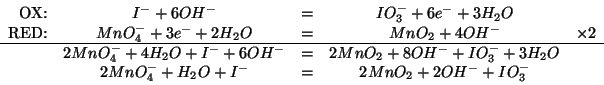
Notate che, siccome il diossido di manganese e' insolubile nell'ambiente di reazione, nelle equazioni viene scritto come tale.
I colori della forma indissociata e dissociata dell'indicatore blu di
bromotimolo (
![]() ) sono rispettivamente
giallo e blu.
) sono rispettivamente
giallo e blu.
![]() di una soluzione di
di una soluzione di ![]() al
al ![]() in peso
(
in peso
(![]() ) vengono diluiti a
) vengono diluiti a ![]() con acqua e alla
soluzione ottenuta si aggiungono alcune gocce dell'indicatore blu di
bromotimolo e
con acqua e alla
soluzione ottenuta si aggiungono alcune gocce dell'indicatore blu di
bromotimolo e ![]() di una soluzione di acido cloridrico
di una soluzione di acido cloridrico
![]() . Calcolare il
. Calcolare il ![]() e indicare il colore della
soluzione:
e indicare il colore della
soluzione:
(
![]() )
)
Dati:

Altri simboli:
|
|
numero di moli iniziale di |
|
|
numero di moli iniziale di |
|
|
massa di |
|
|
massa di soluzione in |
|
|
massa molare di |
| numero di moli iniziale di |
|
| numero di moli iniziale di |
|
| costante di ionizzazione basica dello ione acetato | |
| costante di autoioinizzazione dell'acqua:
|
L'acetato di sodio e' un sale molto solubile in acqua: esso sara'
percio' completamente dissociato in ioni acetato e ioni sodio. Gli
ioni sodio in pratica non hanno caratteristiche acido-base e quindi
non hanno alcuna influenza sul ![]() . Gli ioni acetato, invece, hanno
caratteristiche basiche non trascurabili, poiche'
. Gli ioni acetato, invece, hanno
caratteristiche basiche non trascurabili, poiche' ![]() e' la
base coniugata di
e' la
base coniugata di ![]() , che e' un acido debole. Ci sara'
percio' da considerare l'idrolisi dello ione acetato, che reagisce
con l'acqua da base di Lowry-Brönsted.
, che e' un acido debole. Ci sara'
percio' da considerare l'idrolisi dello ione acetato, che reagisce
con l'acqua da base di Lowry-Brönsted.
Impostiamo l'equilibrio nel modo usuale e prendiamo la concentrazione
di equilibrio degli ioni ![]() come incognita:
come incognita:
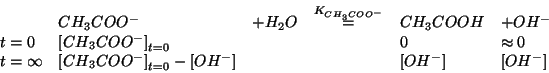
La legge dell'azione di massa e':
La costante di equilibrio della reazione si puo' ricavare facilmente. O ci si ricorda che vale:
da cui:
oppure si puo' partire direttamente dall'espressione generale della costante basica:
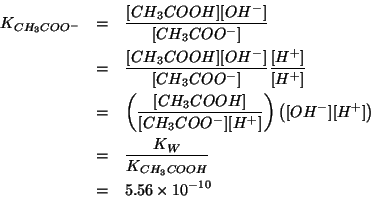
La legge dell'azione di massa sopra scritta e' un'equazione di secondo
grado nell'incognita ![]() e potrebbe essere risolta cosi'
com'e'. Tuttavia, possiamo osservare che il valore numerico della
costante basica
e potrebbe essere risolta cosi'
com'e'. Tuttavia, possiamo osservare che il valore numerico della
costante basica ![]() e' dell'ordine di
e' dell'ordine di
![]() . Questo consente di assumere che la reazione sia molto
poco spostata verso destra e quindi la concentrazione di equilibrio
degli ioni
. Questo consente di assumere che la reazione sia molto
poco spostata verso destra e quindi la concentrazione di equilibrio
degli ioni ![]() sia molto piccola in confronto a quella iniziale
degli ioni acetato. In breve:
sia molto piccola in confronto a quella iniziale
degli ioni acetato. In breve:
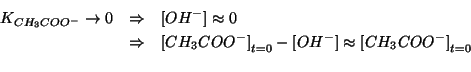
Quindi la legge dell'azione di massa si puo' semplificare in:
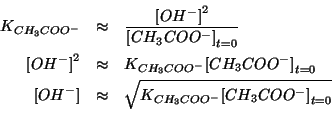
Per trovare
![]() dobbiamo utilizzare la percentuale
in peso e la densita' della soluzione che ci fornisce il testo del
problema.
dobbiamo utilizzare la percentuale
in peso e la densita' della soluzione che ci fornisce il testo del
problema.
Dalla definizione di concentrazione:
Chiaramente, la stechiometria della reazione di dissociazione
dell'acetato di sodio ci dice che
![]() e quindi:
e quindi:
Le moli di acetato di sodio si possono esprimere in funzione della massa e della massa molare:
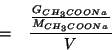
La massa in grammi di acetato di sodio si puo' esprimere in funzione della massa di soluzione (iniziale, prima della diluizione) e della percentuale in massa:
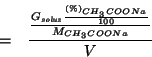
Infine, la massa in grammi di soluzione puo' essere espressa in
funzione della densita' in ![]() e del volume in
e del volume in ![]() :
:
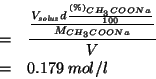
Sostituendo il valore ottenuto piu' sopra si ha:
da cui:
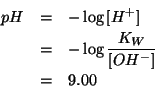
Il ![]() ottenuto e' basico, come ci si aspetta per una soluzione
contenente una base debole (lo ione
ottenuto e' basico, come ci si aspetta per una soluzione
contenente una base debole (lo ione ![]() ).
).
Per sapere di che colore sara' la soluzione, dobbiamo confrontare il
![]() ottentuo con il
ottentuo con il ![]() dell'indicatore. Siccome si ha:
dell'indicatore. Siccome si ha:
ne segue che la concentrazione della forma dissociata dell'indicatore sara' piu' di dieci volte maggiore della concentrazione della sua forma indissociata e quindi la soluzione apparira' del colore della forma dissociata, cioe' nel caso specifico blu.
In seguito all'aggiunta dell'acido cloridrico alla soluzione, si avra' una reazione di neutralizzazione fra l'acido e la base presente. Siccome l'acido cloridrico e' un acido forte, esso sara' completamente dissociato e quindi la reazione ionica netta sara':
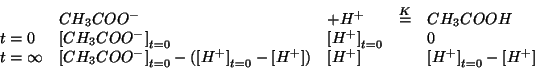
Le concentrazioni di equilibrio devono soddisfare la legge dell'azione di massa:
(e' facile rendersi conto che la costante di equilibrio della reazione e' l'inverso della costante di ionizzazione acida dell'acido acetico)
L'equazione potrebbe essere risolta facilmente rispetto all'incognita
![]() . Tuttavia, basandoci sul fatto che
. Tuttavia, basandoci sul fatto che
![]() e' dell'ordine di
e' dell'ordine di ![]() , possiamo
operare delle semplificazioni. Infatti, se la costante e' molto
grande, la reazione si puo' considerare completa e quindi uno dei due
reagenti (il reagente limitante) verra' quasi completamente consumato,
mentre la concentrazione residua dell'altro si puo' calcolare
facilmente per differenza. Per sapere quale reagente e' in difetto, si
deve confrontare il rapporto molare dei due reagenti con il loro
rapporto stechiometrico (che in questo caso e'
, possiamo
operare delle semplificazioni. Infatti, se la costante e' molto
grande, la reazione si puo' considerare completa e quindi uno dei due
reagenti (il reagente limitante) verra' quasi completamente consumato,
mentre la concentrazione residua dell'altro si puo' calcolare
facilmente per differenza. Per sapere quale reagente e' in difetto, si
deve confrontare il rapporto molare dei due reagenti con il loro
rapporto stechiometrico (che in questo caso e' ![]() ). In breve:
). In breve:
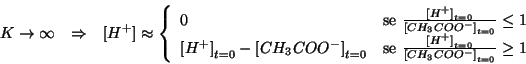
Per il calcolo del rapporto molare, applicando le definizioni apprese durante il corso, si ha:
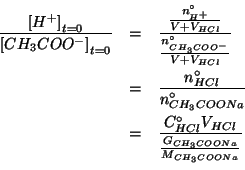
e ripetendo gli stessi passaggi visti alla sezione 1. si arriva a:
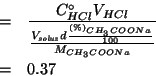
da cui si deduce:
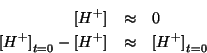
cioe' gli ioni idronio sono in difetto.
Alla luce di questo risultato, la legge dell'azione di massa si puo' semplificare in:
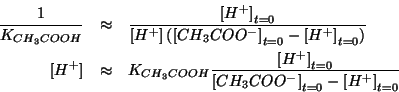
Ripetendo gli stessi passaggi visti per il calcolo del rapporto molare si arriva a:
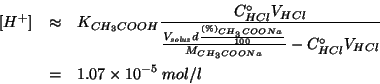
da cui:
Prima di procedere, ritorniamo per un momento alla relazione finale ottenuta:
Questa puo' essere messa in forma logaritmica, prendendo il logaritmo decimale di ambo i membri e cambiando di segno:
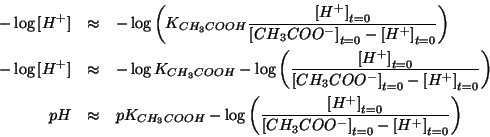
A questa stessa relazione si poteva arrivare direttamente ragionando
come segue. Avendo appurato che gli ioni idrogeno provenienti
dall'acido cloridrico sono in difetto, si conclude che all'equilibrio
si trovera' sia dello ione acetato non reagito che dell'acido acetico
prodotto dalla reazione. Le concentrazioni dell'acido acetico e dello
ione acetato si ottengono facilmente assumendo, come abbiamo visto, la
reazione completa. Allora la soluzione finale sara' una soluzione
tampone, il cui ![]() e' dato proprio dalla relazione:
e' dato proprio dalla relazione:
con
![]() e
e
![]() .
.
Resta infine da rispondere al quesito sul colore della soluzione in
questo caso. Come per il caso precedente, confrontiamo il ![]() trovato con
trovato con ![]() . Si ha:
. Si ha:
Ne segue che la concentrazione della forma indissociata dell'indicatore sara' piu' di dieci volte maggiore della concentrazione della sua forma dissociata e quindi la soluzione apparira' del colore della forma indissociata, cioe' nel caso specifico giallo.