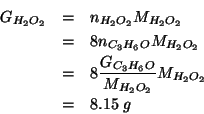next_inactive up previous

21 settembre 2001
Prova scritta di Chimica I

Esercizio 1

$5.0\;g$ di una miscela di zinco e magnesio, bruciati con un eccesso di aria, formano una miscela dei relativi ossidi che pesa $7.0\;g$. Determinare la composizione percentuale in massa della miscela di partenza.

SVOLGIMENTO

Dati:

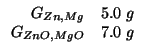
$ \begin{array}{rl} G_{Zn,Mg}&5.0\;g\\ G_{ZnO,MgO}&7.0\;g\\ \end{array}$




Altri simboli:

$G_{Zn}$ massa di $Zn$ in $g$
$G_{Mg}$ massa di $Mg$ in $g$
$G_{ZnO}$ massa di $ZnO$ in $g$
$G_{MgO}$ massa di $MgO$ in $g$
$\MWOf{Zn}$ massa molare di $Zn$ $65.39\;g/mol$
$\MWOf{Mg}$ massa molare di $Mg$ $24.3\;g/mol$
$\MWOf{ZnO}$ massa molare di $ZnO$ $81.39\;g/mol$
$\MWOf{MgO}$ massa molare di $MgO$ $40.3\;g/mol$
$\NOf{Zn}$ numero di moli di $Zn$
$\NOf{Mg}$ numero di moli di $Mg$
$\NOf{ZnO}$ numero di moli di $ZnO$
$\NOf{MgO}$ numero di moli di $MgO$
$\PercentOf{Zn}$ percentuale di $Zn$ nella miscela
$\PercentOf{Mg}$ percentuale di $Mg$ nella miscela




In base ai dati del problema possiamo iniziare a scrivere:

\begin{eqnarray*} G_{Zn}+G_{Mg}&=&G_{Zn,Mg} \end{eqnarray*}

e

\begin{eqnarray*} G_{ZnO}+G_{MgO}&=&G_{ZnO,MgO} \end{eqnarray*}

Siccome si richiede la composizione della miscela, dobbiamo trovare $G_{Zn}$ e $G_{Mg}$. La prima relazione lega direttamente queste due incognite. Ci serve pero' una seconda relazione indipendente: la seconda equazione su scritta serve allo scopo. Infatti essa puo' essere espressa in termini di $G_{Zn}$ e $G_{Mg}$ basandoci sulle seguenti considerazioni.

Innanzitutto, esprimiamo le masse dei due ossidi in termini delle rispettive masse molari e del numero di moli:

\begin{eqnarray*} \NOf{ZnO}\MWOf{ZnO}+\NOf{MgO}\MWOf{MgO}&=&G_{ZnO,MgO} \end{eqnarray*}

Ora, data la formula dei due ossidi e il fatto che la miscela e' stata bruciata in eccesso di ossigeno, possiamo certamente dire che il numero di moli di ciascun ossido deve essere lo stesso del corrispondente elemento nella miscela. Quindi:

\begin{eqnarray*} \NOf{Zn}\MWOf{ZnO}+\NOf{Mg}\MWOf{MgO}&=&G_{ZnO,MgO} \end{eqnarray*}

Ma le moli dei due elementi possono ora essere espresse proprio in termini delle loro masse, portando a:

\begin{eqnarray*} \frac{G_{Zn}}{\MWOf{Zn}}\MWOf{ZnO}+\frac{G_{Mg}}{\MWOf{Mg}}\MWOf{MgO}&=&G_{ZnO,MgO} \end{eqnarray*}

Abbiamo cosi' ottenuto la seconda relazione che lega le due incognite.

Riscriviamo le due equazioni per maggior chiarezza:

\begin{eqnarray*} G_{Zn}+G_{Mg}&=&G_{Zn,Mg}\\ \frac{G_{Zn}}{\MWOf{Zn}}\MWOf{ZnO}+\frac{G_{Mg}}{\MWOf{Mg}}\MWOf{MgO}&=&G_{ZnO,MgO}\\ \end{eqnarray*}

Non resta che risolvere il sistema.

Sottraendo dalla prima la seconda moltiplicata per $\frac{\MWOf{Zn}}{\MWOf{ZnO}}$ si ottiene:

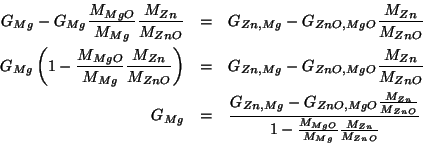
\begin{eqnarray*} G_{Mg}-G_{Mg}\frac{\MWOf{MgO}}{\MWOf{Mg}}\frac{\MWOf{Zn}}{\MWO... ...}{1-\frac{\MWOf{MgO}}{\MWOf{Mg}}\frac{\MWOf{Zn}}{\MWOf{ZnO}}}\\ \end{eqnarray*}

Moltiplicando ambo i membri per $\frac{100}{G_{Zn,Mg}}$ si ottiene direttamente la percentuale di $Mg$ nella miscela:

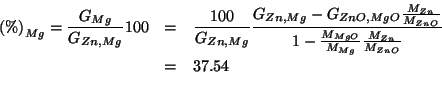
\begin{eqnarray*} \PercentOf{Mg}=\frac{G_{Mg}}{G_{Zn,Mg}}100&=&\frac{100}{G_{Zn,... ...WOf{MgO}}{\MWOf{Mg}}\frac{\MWOf{Zn}}{\MWOf{ZnO}}}\\ &=&37.54\\ \end{eqnarray*}

Chiaramente:

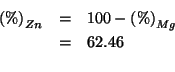
\begin{eqnarray*} \PercentOf{Zn}&=&100-\PercentOf{Mg}\\ &=&62.46\\ %(- 100.0 37.54)62.46 \end{eqnarray*}

Esercizio 2

Si hanno $100\;ml$ di una soluzione di un generico acido forte $HX$ in concentrazione $0.01\;mol/l$. Calcolare il valore del $pH$ quando si aggiunge un volume di una soluzione di ammoniaca $0.01\;mol/l$:

  1. corrispondente ai $\frac{2}{3}$ del volume dell'acido
  2. uguale al volume dell'acido
  3. in eccesso di $\frac{1}{3}$ rispetto al volume dell'acido

( $K_{NH_3}=1.8\times10^{-5}$)

SVOLGIMENTO

Dati:

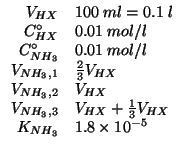
$ \begin{array}{rl} \VOf{HX}&100\;ml=0.1\;l\\ \CZeroOf{HX}&0.01\;mol/l\\ \CZer... ...3,3}&\VOf{HX}+\frac{1}{3}\VOf{HX}\\ \KOf{NH_3}&1.8\times10^{-5}\\ \end{array}$




Altri simboli:

$K_{W}$ costante di autoionizzazione dell'acqua: $1\times10^{-14}$




Come osservazione preliminare, consideriamo la reazione che si verifica all'atto dell'aggiunta dell'ammoniaca:

\begin{eqnarray*} NH_3+H^+&=&NH_4^+ \end{eqnarray*}

La costante di equilibrio $K$ di questa reazione si esprime facilmente in termini di dati del problema:

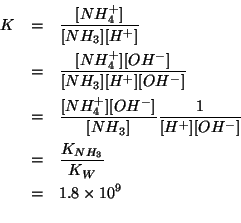
\begin{eqnarray*} K&=&\frac{\ConcOf{NH_4^+}}{\ConcOf{NH_3}\ConcOf{H^+}}\\ &=&\f... ...oncOf{OH^-}}\\ &=&\frac{\KOf{NH_3}}{K_W}\\ &=&1.8\times10^9\\ \end{eqnarray*}

Dal valore di $K$ si deduce che la reazione si puo' considerare completa.

Caso a.

Siccome la quantita' di ammoniaca e' inferiore a quella di acido (dato che le concentrazioni delle due soluzioni sono uguali), considerando la reazione fra ioni idronio e ammoniaca completa, la base e' il reagente limitante. Allora il calcolo del $pH$ e' immediato.

Dopo la reazione rimarranno ioni idronio non reagiti in concentrazione pari a:

\begin{eqnarray*} \ConcOf{H^+}&=&\InitialConcOf{H^+}-\InitialConcOf{NH_3} \end{eqnarray*}

Le concentrazioni iniziali da considerare non sono quelle date nel testo dell'esercizio, ma si deve tenere conto della diluizione dovuta al mescolamento delle due soluzioni. Quindi:

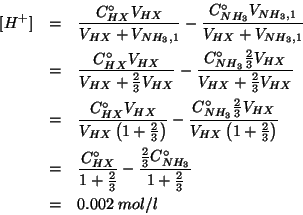
\begin{eqnarray*} \ConcOf{H^+}&=&\frac{\CZeroOf{HX}\VOf{HX}}{\VOf{HX}+\VOf{NH_3,... ...rac{\frac{2}{3}\CZeroOf{NH_3}}{1+\frac{2}{3}}\\ &=&0.002\;mol/l \end{eqnarray*}

e:

\begin{eqnarray*} pH&=&-\log\ConcOf{H^+}\\ &=&2.7\end{eqnarray*}

Il risultato e' ragionevole. Infatti, il $pH$ e' aumentato rispetto al valore iniziale in presenza del solo acido ( $\CZeroOf{HX}=10^{-2}\;mol/l\Rightarrow{}pH=2$): questo e' cio' che ci aspettiamo in seguito all'aggiunta di una base.

Caso b.

In questo caso acido e base sono in rapporto stechiometrico e quindi non possiamo considerare completa la reazione fra essi (altrimenti otterremmo una concentrazione di ioni idronio nulla).

Impostiamo dunque il consueto trattamento dell'equilibrio, osservando, comunque, che le concentrazioni iniziali di ioni idronio e ammoniaca sono uguali e quindi tali saranno anche i corrispondenti valori di equilibrio:




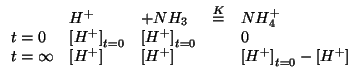
$ \begin{array}{lllll} &{H^+}&+{NH_3}&\stackrel{K}{=}&NH_4^+\\ t=0&\InitialConc... ...\ConcOf{{H^+}}&\ConcOf{{H^+}}&&\InitialConcOf{{H^+}}-\ConcOf{{H^+}} \end{array}$

La legge dell'azione di massa e':

\begin{eqnarray*} K&=&\frac{\InitialConcOf{{H^+}}-\ConcOf{{H^+}}}{\ConcOf{{H^+}}^2} \end{eqnarray*}

Questa equazione puo' essere risolta cosi' com'e'. Tuttavia possiamo semplificarla se osserviamo che, essendo la costante di equilibrio molto grande, la concentrazione di ioni idronio ``sopravvissuti'' all'equilibrio sara' molto piccola in confronto al suo valore iniziale. In sintesi:

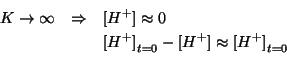
\begin{eqnarray*} K\rightarrow\infty&\Rightarrow&\ConcOf{{H^+}}\approx0\\ &&\InitialConcOf{{H^+}}-\ConcOf{{H^+}}\approx\InitialConcOf{{H^+}}\\ \end{eqnarray*}

Cosi', la legge dell'azione di massa si semplifica in:

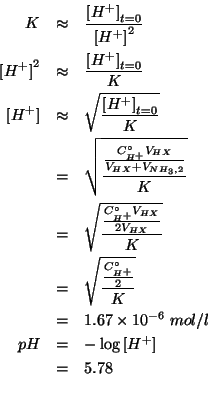
\begin{eqnarray*} K&\approx&\frac{\InitialConcOf{{H^+}}}{\ConcOf{{H^+}}^2}\\ \C... ...\ &=&5.78\\ %(-(log10 1.6666666666666667e-06))5.778151250383644 \end{eqnarray*}

Osserviamo che il valore trovato per $\ConcOf{{H^+}}$ e' tale da giustificare ampiamente l'approssimazione $\InitialConcOf{{H^+}}-\ConcOf{{H^+}}\approx\InitialConcOf{{H^+}}$.

La risoluzione di questo punto si poteva anche impostare facendo reagire idealmente l'acido e la base in modo completo costruendo pertanto delle condizioni iniziali equivalenti a quelle date:




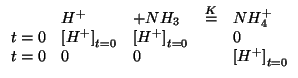
$ \begin{array}{lllll} &{H^+}&+{NH_3}&\stackrel{K}{=}&NH_4^+\\ t=0&\InitialConcOf{{H^+}}&\InitialConcOf{H^+}&&0\\ t=0&0&0&&\InitialConcOf{{H^+}} \end{array}$

Il sistema cosi' ottenuto e' il ben noto caso della dissociazione di un acido debole ($NH_4^+$) di data concentrazione iniziale (la reazione procedera' da destra verso sinistra, con costante di equilibrio pari a $1/K$). Chiaramente, applicando la nota formula relativa a questo caso, si ottiene un'espressione identica a quella ottenuta in precedenza.

Caso c.

In questo caso l'ammoniaca e' in eccesso. Se consideriamo la reazione completa, allora l'acido e' il reagente limitante. Questo significa che la concentrazione all'equilibrio degli ioni idronio sara' praticamente nulla. D'altro canto, e' proprio tale concentrazione che ci interessa.

Una prima strategia parte dalla seguente considerazione. Se ammettiamo che la reazione sia completa, allora una parte dell'ammoniaca (precisamente un numero di moli pari a quello delle moli di acido inizialmente presenti) verra' trasformata in ione ammonio e una parte restera' non reagita; dopo la reazione, la soluzione conterra' pertanto una quantita' apprezzabile di ammoniaca (base) e ione ammonio (acido coniugato): in altre parole si tratta di una soluzione tampone. Bastera' allora applicare il noto risultato che fornisce immediatamente il $pOH$ di un tampone basico. In definitiva:




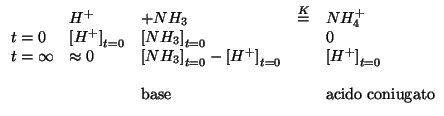
$ \begin{array}{lllll} &{H^+}&+{NH_3}&\stackrel{K}{=}&NH_4^+\\ t=0&\InitialConc... ...alConcOf{{H^+}}\\ &&&&\\ &&\mbox{base}&&\mbox{acido coniugato}\\ \end{array}$

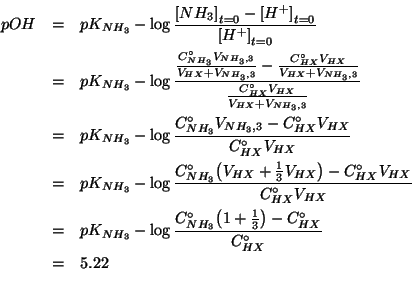
\begin{eqnarray*} pOH&=&pK_{NH_3}-\log{\frac{\InitialConcOf{NH_3}-\InitialConcOf... ...(- (* c0nh3 (+ 1.0 (/ 1.0 3.0))) c0hx) c0hx))))5.221848749616356 \end{eqnarray*}

da cui:

\begin{eqnarray*} pH&=&14.0-pOH\\ &=&8.78\end{eqnarray*}

Come ci si aspetta (abbiamo aggiunto un eccesso di base), il $pH$ trovato e' basico.

Un secondo modo equivalente di procedere consiste nell'impostare la trattazione dell'equilibrio nel modo consueto, sfruttando poi il valore molto grande della costante di equilibrio.

Scegliendo la concentrazione di ioni idronio all'equilibrio come incognita si ha:

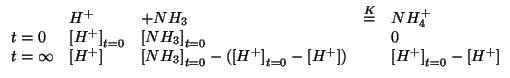
$ \begin{array}{lllll} &H^+&+{NH_3}&\stackrel{K}{=}&NH_4^+\\ t=0&\InitialConcOf... ...oncOf{H^+}-\ConcOf{H^+}\right)&&\InitialConcOf{H^+}-\ConcOf{H^+}\\ \end{array}$

Inseriamo le concentrazioni di equilibrio nella legge dell'azione di massa:

\begin{eqnarray*} K&=&\frac{\InitialConcOf{H^+}-\ConcOf{H^+}}{\ConcOf{H^+}\left(... ...ncOf{NH_3}-\left(\InitialConcOf{H^+}-\ConcOf{H^+}\right)\right)} \end{eqnarray*}

Ora osserviamo che, essendo la costante molto grande, la concentrazione di ioni idronio ``sopravvissuta'' ad equilibrio raggiunto sara' talmente piccola da essere trascurabile rispetto alla concentrazione inizialmente presente. In sintesi:

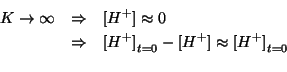
\begin{eqnarray*} K\rightarrow\infty&\Rightarrow&\ConcOf{H^+}\approx0\\ &\Rightarrow&\InitialConcOf{H^+}-\ConcOf{H^+}\approx\InitialConcOf{H^+}\\ \end{eqnarray*}

Introducendo questa approssimazione nella legge dell'azione di massa si ottiene:

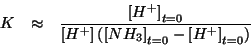
\begin{eqnarray*} K&\approx&\frac{\InitialConcOf{H^+}}{\ConcOf{H^+}\left(\InitialConcOf{NH_3}-\InitialConcOf{H^+}\right)}\\ \end{eqnarray*}

che puo' essere riarrangiata come segue:

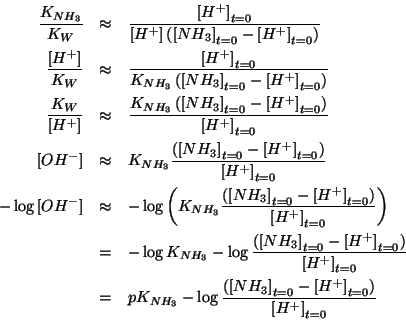
\begin{eqnarray*} \frac{K_{NH_3}}{K_W}&\approx&\frac{\InitialConcOf{H^+}}{\ConcO... ...ConcOf{NH_3}-\InitialConcOf{H^+}\right)}{\InitialConcOf{H^+}}\\ \end{eqnarray*}

che e' identica all'espressione scritta prima considerando il sistema come una soluzione tampone (e quindi porta al medesimo risultato).

Esercizio 3

Calcolare quanti grammi di acqua ossigenata ($H_2O_2$) sono necessari per ossidare $1.74\;g$ di acetone ($C_3H_6O$) ad anidride carbonica ed acqua in ambiente acido. (L'acqua ossigenata si riduce ad acqua).

SVOLGIMENTO

Dati:

$ \begin{array}{rl} \GOf{C_3H_6O}&1.74\;g\\ \end{array}$




Altri simboli:

$\MWOf{C_3H_6O}$ massa molare dell'acetone: $58.08\;g/mol$
$\MWOf{H_2O_2}$ massa molare dell'acqua ossigenata: $34.01\;g/mol$
$\NOf{H_2O_2}$ numero di moli $H_2O_2$
$\NOf{C_3H_6O}$ numero di moli $C_3H_6O$
$\GOf{H_2O_2}$ massa di $H_2O_2$ richiesta in $g$




Prima di tutto dobbiamo scrivere l'equazione chimica bilanciata che descrive la reazione. Applicando la procedura vista durante il corso si ha:


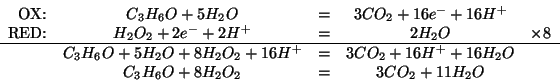
\begin{displaymath} \begin{array}{rcccr} \mbox{OX:}&C_3H_6O+5H_2O&=&3CO_2+16e^-+... ...6H^++16H_2O&\\ &C_3H_6O+8H_2O_2&=&3CO_2+11H_2O&\\ \end{array}\end{displaymath}

Dall'equazione si vede che il rapporto stechiometrico fra $H_2O_2$ e $C_3H_6O$ e' pari a $8$. Quindi:

\begin{eqnarray*} \GOf{H_2O_2}&=&\NOf{H_2O_2}\MWOf{H_2O_2}\\ &=&8\NOf{C_3H_6O}\... ..._2}\\ &=&8.15\;g %(* 8.0 (/ 1.74 58.08) 34.01)8.151157024793388 \end{eqnarray*}

next_inactive up previous