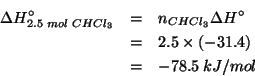Per l'aldeide formica (![]() ):
):
| Elettroni di valenza | |
| carica | 0 |
| totale | |
Siccome un atomo di idrogeno non puo' mai essere l'atomo centrale, e il carbonio e' meno elettronegativo dell'ossigeno, il primo passo verso la scrittura della formula di Lewis e':
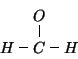
In tal modo abbiamo sistemato ![]() dei
dei ![]() elettroni di valenza
della molecola. Completiamo ora gli ottetti elettronici attorno agli
atomi terminali (ovviamente non attorno agli atomi di
idrogeno):
elettroni di valenza
della molecola. Completiamo ora gli ottetti elettronici attorno agli
atomi terminali (ovviamente non attorno agli atomi di
idrogeno):
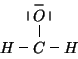
Abbiamo cosi' sistemato tutti i ![]() elettroni di valenza della
molecola. Tuttavia, l'atomo centrale non e' circondato da otto
elettroni; allora usiamo un doppietto di non legame dell'atomo di
ossigeno per formare un legame
elettroni di valenza della
molecola. Tuttavia, l'atomo centrale non e' circondato da otto
elettroni; allora usiamo un doppietto di non legame dell'atomo di
ossigeno per formare un legame ![]() con l'atomo di
con l'atomo di ![]() :
:
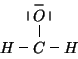
Quella ottenuta e' una struttura di Lewis perfettamente lecita: tutti gli atomi (tranne ovviamente gli atomi di idrogeno) rispettano la regola dell'ottetto. E' facile rendersi conto che qualsiasi ridistribuzione degli elettroni produce una struttura non conforme alle regole di Lewis: possiamo quindi dire che la struttura ottenuta sara' anche la piu' stabile. Possiamo verificare cio' determinando le cariche atomiche formali.
| Elettroni di valenza | |
E' chiaro che, nella formula di Lewis data, tutti gli atomi della molecola hanno gli stessi elettroni di valenza che presentano quando sono isolati: ne segue che tutte le cariche atomiche formali sono nulle. Questa e' la condizione di massima stabilita', come avevamo previsto.
| coppie strutturali | 3 |
| geometria delle coppie strutturali | trigonale planare |
| modello |
 |
| coppie di non legame | 0 |
| geometria molecolare | trigonale planare |
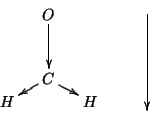
Si capisce facilmente che la molecola deve essere polare e che il momento di dipolo risultante sara' orientato come mostrato sopra.
Per la formula di Lewis che ci apprestiamo a descrivere, abbiamo gia' trovato quanti elettroni di valenza ha ciascun atomo nella molecola:
Siccome la geometria delle coppie strutturali e' trigonale planare,
l'atomo di carbonio presentera' un'ibridazione di tipo ![]() ,
ottenuta combinando l'orbitale di valenza
,
ottenuta combinando l'orbitale di valenza ![]() con due dei tre
orbitali
con due dei tre
orbitali ![]() . Rimane sull'atomo centrale un orbitale
. Rimane sull'atomo centrale un orbitale ![]() puro
normale al piano contenente i tre orbitali ibridi. Dalla formula di
Lewis si vede che l'atomo di
puro
normale al piano contenente i tre orbitali ibridi. Dalla formula di
Lewis si vede che l'atomo di ![]() deve formare
deve formare ![]() legami
legami
![]() e
e ![]() legame
legame ![]() ; quindi, i
; quindi, i ![]() orbitali ibridi e
l'orbitale
orbitali ibridi e
l'orbitale ![]() puro dovranno essere semioccupati per formare i
puro dovranno essere semioccupati per formare i ![]() legami
legami ![]() e il legame
e il legame ![]() , rispettivamente. Cio' si
realizza assegnando ciascuno dei
, rispettivamente. Cio' si
realizza assegnando ciascuno dei ![]() elettroni di valenza dell'atomo
di carbonio ad un orbitale diverso.
elettroni di valenza dell'atomo
di carbonio ad un orbitale diverso.
Sistemando i ![]() elettroni di valenza dell'atomo di ossigeno
secondo il principio di Pauli e la regola di Hund, si ottengono
elettroni di valenza dell'atomo di ossigeno
secondo il principio di Pauli e la regola di Hund, si ottengono ![]() orbitali
orbitali ![]() semioccupati: uno di essi avra' simmetria
semioccupati: uno di essi avra' simmetria ![]() e
sovrapporra' con un orbitale ibrido dell'atomo di carbonio;
l'altro avra' simmetria
e
sovrapporra' con un orbitale ibrido dell'atomo di carbonio;
l'altro avra' simmetria ![]() e potra' sovrapporsi all'orbitale
e potra' sovrapporsi all'orbitale
![]() puro dell'atomo di carbonio.
puro dell'atomo di carbonio.
Ciascun atomo di idrogeno possiede ![]() elettrone di valenza che
verra' sistemato nell'orbitale
elettrone di valenza che
verra' sistemato nell'orbitale ![]() , che potra' sovrapporsi con il
relativo orbitale ibrido dell'atomo di carbonio. Gli elettroni di
ciascun legame vanno indicati con spin antiparallelo.
, che potra' sovrapporsi con il
relativo orbitale ibrido dell'atomo di carbonio. Gli elettroni di
ciascun legame vanno indicati con spin antiparallelo.
Ne risulta il seguente schema:
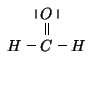
![\begin{psfrags}\psfrag{C} [c][c]{C}\psfrag{H} [c][c]{H}\psfrag{O} [c][c]{O...
...[c]{{$sp^2$}}\psfrag{p} [c][c]{{$p$}}
\includegraphics{h2co.eps}
\end{psfrags}](img27.gif)
Le seguenti sostanze sono tutte solubili in benzene e non si
dissociano. In esperimenti separati ![]() di ciascuna viene
aggiunto a
di ciascuna viene
aggiunto a ![]() di benzene. Quale sostanza da' una soluzione
con il piu' basso punto di congelamento?
di benzene. Quale sostanza da' una soluzione
con il piu' basso punto di congelamento?
Dati:
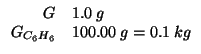
Altri simboli:
|
|
abbassamento crioscopico in |
| costante crioscopica del benzene in |
|
| molalita' del composto |
|
| numero di moli del composto |
|
| massa molare del composto |
L'espressione per l'abbassamento crioscopico dovuto al composto ![]() e':
e':
Ora esprimiamo la molalita' in base ai dati del problema:
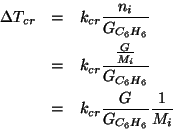
Il termine
![]() e' chiaramente una costante: ne
segue che l'abbassamento crioscopico e' inversamente proporzionale
alla massa molare. Cioe': il composto con la massa molare minore dara'
l'abbassamento crioscopico maggiore.
e' chiaramente una costante: ne
segue che l'abbassamento crioscopico e' inversamente proporzionale
alla massa molare. Cioe': il composto con la massa molare minore dara'
l'abbassamento crioscopico maggiore.
Le masse molari sono ottenute immediatamente con l'aiuto della tavola periodica:

Quindi l'abbassamento crioscopico maggiore si avra' con il composto
numero ![]() (l'idrazina).
(l'idrazina).
Dati:
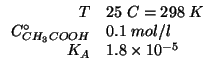
Altri simboli:
| costante dei gas:
|
La pressione osmotica e' una proprieta' colligativa e come tale e'
determinata dalla concentrazione totale di particelle originate
in soluzione dal soluto.
L'acido acetico e' un acido debole che si dissocia parzialmente secondo:
All'equilibrio la soluzione conterra' quindi acido acetico indissociato, ioni acetato e ioni idrogeno: la pressione osmotica della soluzione sara' determinata dalla somma delle concentrazioni di queste tre specie.
L'espressione per il calcolo della pressione osmotica e':
Per quanto appena detto, la concentrazione molare colligativa ![]() e'
data da:
e'
data da:
Il problema si sposta dunque alla determinazione delle concentrazioni di equilibrio delle tre specie legate dall'equazione di dissociazione dell'acido acetico.
La dissociazione di un acido debole in soluzione acquosa e' stata trattata durante il corso:
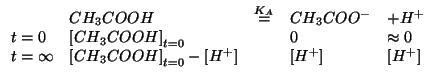
Le concentrazioni di equilibrio devono soddisfare la legge dell'azione
di massa:
A questo punto si puo' risolvere l'equazione quadratica risultante. Tuttavia, questa puo' essere ulteriormente semplificata trascurando la concentrazione di acido dissociato rispetto alla sua concentrazione iniziale, dato il valore piuttosto piccolo della costante di ionizzazione:
da cui si ottiene il risultato finale per
![]() :
:
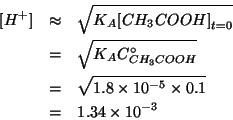
Sostituendo piu' sopra il valore trovato si ottengono le concentrazioni di equilibrio per le altre due specie:
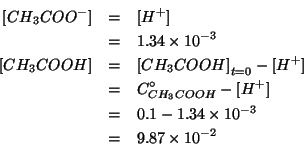
Notate come il valore di equilibrio della concentrazione di acido acetico indissociato sia praticamente identico a quello iniziale: cio' giustifica l'approssimazione fatta per semplificare la legge dell'azione di massa.
Sostituendo infine nell'espressione per la pressione osmotica si ha:
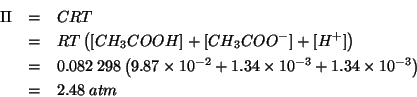
Dati:
![]()
Altri simboli:
| massa molare del cloruro di sodio: |
|
| numero di moli di cloruro di sodio | |
| numero di molecole di cloruro di sodio | |
| Numero di Avogadro:
|
In pratica, si deve trovare quante molecole di cloruro di sodio sono
contenute in una massa pari a ![]() . Dalla definizione
di mole e massa molare si ha direttamente:
. Dalla definizione
di mole e massa molare si ha direttamente:
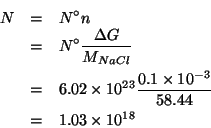
cioe': un errore di ![]() mentre si pesa del cloruro di
sodio significa un errore di piu' o meno un miliardo di
miliardi di molecole!
mentre si pesa del cloruro di
sodio significa un errore di piu' o meno un miliardo di
miliardi di molecole!
Dalla tavola periodica si vede che l'ossigeno ha numero atomico pari a
![]() . La sua configurazione elettronica dello stato fondamentale
sara' pertanto:
. La sua configurazione elettronica dello stato fondamentale
sara' pertanto:
![]() , ovvero, con la notazione a
caselle:
, ovvero, con la notazione a
caselle:
|
|
|
|
|
|
Notate che, per la regola di Hund, i quattro elettroni di tipo ![]() vanno disposti in modo che due di essi siano spaiati con spin parallelo.
vanno disposti in modo che due di essi siano spaiati con spin parallelo.
Dati:

Altri simboli:
| massa molare dell'elemento in |
Dai dati del problema possiamo ricavare immediatamente la massa molare dell'elemento:
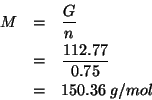
Usando la tavola periodica si trova che la massa molare ottenuta e'
quella del samario (![]() ).
).
Dati:
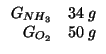
Altri simboli:
| massa molare dell'ammoniaca: |
|
| massa molare dell'ossigeno: |
|
| massa molare dell'acqua: |
|
| numero di moli di ammoniaca | |
| numero di moli di ossigeno | |
| numero di moli di acqua | |
| massa di acqua in |
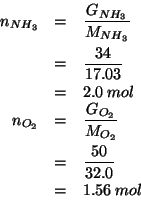
Se i due reagenti fossero in rapporto stechiometrico, il loro rapporto
molare dovrebbe essere: ![]() . Il rapporto molare per le
quantita' date e':
. Il rapporto molare per le
quantita' date e': ![]() , cioe' minore di quello
stechiometrico. Ne segue che il reagente limitante e' l'ammoniaca.
, cioe' minore di quello
stechiometrico. Ne segue che il reagente limitante e' l'ammoniaca.
Siccome il reagente limitante e' l'ammoniaca, la quantita' d'acqua che si puo' formare e' determinata dalla quantita' di ammoniaca. In particolare, dal rapporto stechiometrico ammoniaca/acqua:
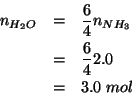
e quindi:
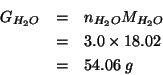
La reazione coinvolge le due coppie redox
![]() e
e
![]() : la prima reagisce nel verso della riduzione, la seconda
in quello dell'ossidazione.
: la prima reagisce nel verso della riduzione, la seconda
in quello dell'ossidazione.
Applicando il metodo visto durante il corso si ha:
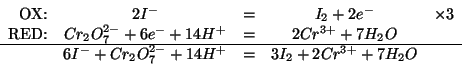
Un tampone viene preparato miscelando ![]() di Tris con
di Tris con
![]() di
di ![]() in un volume di
in un volume di ![]() . Calcolate il
. Calcolate il
![]() della soluzione.
della soluzione.
Dati:
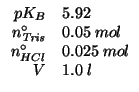
Altri simboli:
| costante di equilibrio della reazione
|
|
| costante di ionizzazione acida di
|
|
| costante di autoionizzazione dell'acqua:
|
|
|
|
numero di moli di |
|
|
numero di moli di |
Il tampone viene preparato mescolando una base debole con una quantita' in difetto di un acido forte: l'acido coniugato della base debole necessario affinche' la soluzione abbia caratteristiche di tampone si forma pertanto in seguito alla reazione:
in cui gli ioni idrogeno provengono dalla dissociazione totale dell'acido cloridrico.
La reazione su scritta e' praticamente completa; infatti la sua
costante di equilibrio e' l'inversa della costante di ionizzazione
acida della specie
![]() , che, a sua volta, e' data dal
rapporto fra la costante di autoionizzazione dell'acqua e la costante
di ionizzazione basica della base debole:
, che, a sua volta, e' data dal
rapporto fra la costante di autoionizzazione dell'acqua e la costante
di ionizzazione basica della base debole:
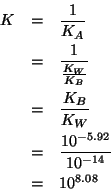
Da cio' e dal fatto che gli ioni idrogeno sono chiaramente il reagente
limitante, segue che i numeri di moli di ![]() e
e
![]() dopo la reazione saranno:
dopo la reazione saranno:
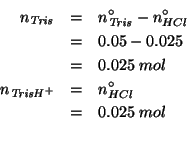
Infine, il ![]() della soluzione risultante puo' essere ricavato
immediatamente utilizzando la formula (ricavata durante il corso) che
si applica ad un tampone basico:
della soluzione risultante puo' essere ricavato
immediatamente utilizzando la formula (ricavata durante il corso) che
si applica ad un tampone basico:
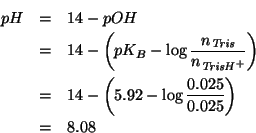
L'entalpia standard di formazione del cloroformio liquido a ![]() e'
e'
![]() e quella del cloroformio gassoso alla stessa
temperatura e' di
e quella del cloroformio gassoso alla stessa
temperatura e' di
![]() . Determinare la variazione di
entalpia standard per la condensazione di
. Determinare la variazione di
entalpia standard per la condensazione di ![]() di cloroformio
a
di cloroformio
a ![]() .
.
Dati:
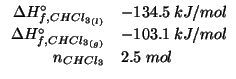
Altri simboli:
|
|
variazione di entalpia molare standard |
|
|
variazione di entalpia standard
per |
Il processo da considerare e':
la cui variazione di entalpia molare in condizioni standard a
![]() e' data da:
e' data da:
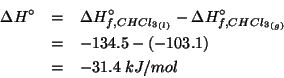
Quindi: