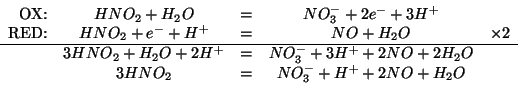![]() ,
, ![]() e
e ![]() sono tre composti binari di
molibdeno e zolfo; l'atomo di molibdeno ha una massa pari a tre volte
quella dell'atomo di zolfo. Senza fare uso dei valori numerici delle
masse molari individuali del molibdeno e dello zolfo:
sono tre composti binari di
molibdeno e zolfo; l'atomo di molibdeno ha una massa pari a tre volte
quella dell'atomo di zolfo. Senza fare uso dei valori numerici delle
masse molari individuali del molibdeno e dello zolfo:
Dati:
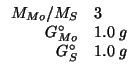
Altri simboli:
| numero di moli di molibdeno | |
| numero di moli di zolfo | |
| massa di molibdeno in |
|
| massa di zolfo in |
In pratica, il problema richiede di trovare i rapporti ![]() e
e ![]() per una quantita' arbitraria di ciascuno dei tre
composti.
per una quantita' arbitraria di ciascuno dei tre
composti.
I rapporti tra le masse si possono trovare facilmente a partire dai rapporti molari, utilizzando il fatto che si conosce il rapporto fra le masse molari di molibdeno e zolfo.
Cosi', per il composto ![]() :
:
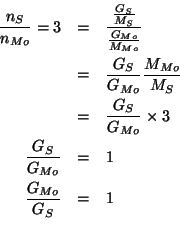
Cioe': in ![]() , per
, per ![]() di molibdeno si combina una massa
di zolfo pari
di molibdeno si combina una massa
di zolfo pari ![]() e per
e per ![]() di zolfo si combina una massa
di molibdeno pari
di zolfo si combina una massa
di molibdeno pari ![]() .
.
In modo perfettamente analogo si procede per gli altri due composti.
Per ![]() :
:
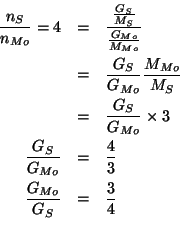
e per ![]() :
:
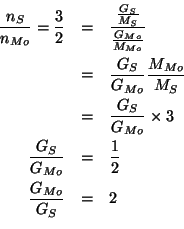
Il lutezio (![]() ) e' un solido con una densita' pari a
) e' un solido con una densita' pari a
![]() nelle normali condizioni di temperatura e
pressione. Calcolate il volume che ogni atomo di lutezio ha a sua
disposizione nel solido.
nelle normali condizioni di temperatura e
pressione. Calcolate il volume che ogni atomo di lutezio ha a sua
disposizione nel solido.
Dati:
![]()
Altri simboli:
| volume per atomo di lutezio | |
| volume molare del lutezio | |
| massa molare del lutezio:
|
|
| numero di Avogadro:
|
Consideriamo una massa di lutezio pari alla sua massa molare: il volume occupato da questa massa (il cosiddetto volume molare) si ricava immediatamente dalla densita' data; d'altro canto, il numero di atomi di lutezio contenuto in una massa pari alla sua massa molare e', per definizione, il numero di Avogadro. Quindi, dividendo il volume molare del lutezio per il numero di Avogadro si ottiene il risultato.
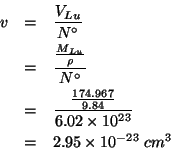
![]() di idrogeno vengono mescolati con
di idrogeno vengono mescolati con ![]() di ossigeno; i
due gas reagiscono completamente per formare acqua. Calcolate la
quantita' di acqua formata in grammi.
di ossigeno; i
due gas reagiscono completamente per formare acqua. Calcolate la
quantita' di acqua formata in grammi.
Dati:
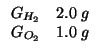
Altri simboli:
| massa di acqua in |
|
| numero di moli di idrogeno | |
| numero di moli di ossigeno | |
| massa molare dell'idrogeno: |
|
| massa molare dell'ossigeno: |
|
| numero di moli di acqua | |
| massa molare dell'acqua: |
Per prima cosa scriviamo l'equazione bilanciata per la reazione:
Siccome si tratta di una reazione completa, dovremo individuare il reagente limitante. A questo scopo valutiamo il rapporto molare con cui sono stati mescolati idrogeno e ossigeno e confrontiamolo col rapporto stechiometrico.
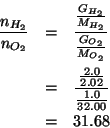
Vediamo che il rapporto trovato e' ben maggiore di quello
stechiometrico (che e' ![]() ): cio' significa che il reagente
limitante e' l'ossigeno. Allora, la massima quantita' di acqua
ottenibile e' legata al numero di moli di ossigeno dalla stechiometria
della reazione:
): cio' significa che il reagente
limitante e' l'ossigeno. Allora, la massima quantita' di acqua
ottenibile e' legata al numero di moli di ossigeno dalla stechiometria
della reazione:
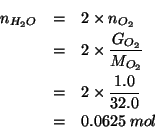
e quindi:
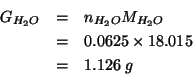
Certe bottiglie di vetro sottile possono sopportare una differenza di
pressione rispetto all'esterno pari a ![]() prima di
esplodere. Una bottiglia di questo tipo viene sigillata alla
temperatura di
prima di
esplodere. Una bottiglia di questo tipo viene sigillata alla
temperatura di ![]() in una giornata in cui la pressione
atmosferica e' di
in una giornata in cui la pressione
atmosferica e' di ![]() ; viene quindi introdotta in una stufa
e riscaldata. Calcolate la temperatura a cui la bottiglia esplodera'.
; viene quindi introdotta in una stufa
e riscaldata. Calcolate la temperatura a cui la bottiglia esplodera'.
Dati:
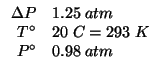
Altri simboli:
| la temperatura cercata | |
| costante dei gas:
|
In pratica, dobbiamo calcolare a quale temperatura la pressione
all'interno della bottiglia raggiungera' un valore pari
![]() : in tal caso, infatti, la pressione interna
della bottiglia superera' quella esterna di
: in tal caso, infatti, la pressione interna
della bottiglia superera' quella esterna di
![]() e
la bottiglia esplodera'.
e
la bottiglia esplodera'.
Il calcolo viene fatto utilizzando la legge dei gas ideali, che, siccome il numero di moli e il volume restano costanti, possiamo scrivere convenientemente come:
ovvero:
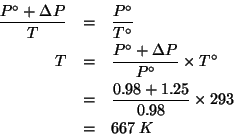
Quando ![]() di uno zucchero, non volatile e non elettrolita,
vengono disciolti in
di uno zucchero, non volatile e non elettrolita,
vengono disciolti in ![]() d'acqua, il punto di ebollizione
dell'acqua aumenta di
d'acqua, il punto di ebollizione
dell'acqua aumenta di ![]() . Calcolate la massa molare dello
zucchero.
. Calcolate la massa molare dello
zucchero.
La costante ebullioscopica dell'acqua e'
![]() .
.
Dati:
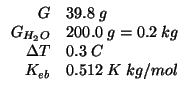
Altri simboli:
| massa molare cercata | |
| numero di moli di zucchero | |
| molalita' della soluzione |
Cominciamo a scrivere la formula per l'innalzamento ebullioscopico:
Ora basta esprimere la molalita' in funzione della massa molare cercata:
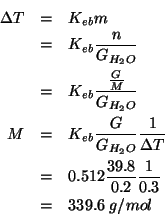
La costante di equilibrio per la reazione del cosiddetto ``gas d'acqua'':
e' pari a ![]() alla temperatura di
alla temperatura di ![]() .
.
Calcolate il quoziente di reazione ![]() per ciascuna delle seguenti
condizioni (
per ciascuna delle seguenti
condizioni (![]() , tutte le pressioni parziali espresse in
, tutte le pressioni parziali espresse in
![]() ) e stabilite in che verso evolvera' la reazione:
) e stabilite in che verso evolvera' la reazione:
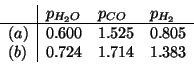
Dati:
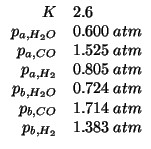
Altri simboli:
| quoziente di reazione per le condizioni (a) | |
| quoziente di reazione per le condizioni (b) |
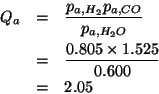
Siccome ![]() , la reazione procedera' verso destra.
, la reazione procedera' verso destra.
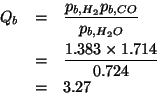
Siccome ![]() , la reazione procedera' verso sinistra.
, la reazione procedera' verso sinistra.
Il cloridrato di papaverina (
![]() ) e' un farmaco usato
come rilassante muscolare ed e' un acido debole monoprotico. Una
soluzione preparata sciogliendo in acqua
) e' un farmaco usato
come rilassante muscolare ed e' un acido debole monoprotico. Una
soluzione preparata sciogliendo in acqua ![]() di
di
![]() e portando il volume a
e portando il volume a ![]() ha un
ha un
![]() . Calcolate il
. Calcolate il ![]() di
di
![]() .
.
Dati:

Altri simboli:
| concentrazione iniziale dell'acido |
La reazione di ionizzazione del cloridrato di papaverina e':
La formula ricavata durante il corso per la concentrazione di ioni idrogeno in una soluzione di un acido debole monoprotico e':
che puo' essere esplicitata rispetto alla costante di ionizzazione acida:
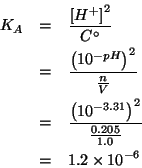
Calcolate la concentrazione di ![]() all'equilibrio in una
soluzione preparata sciogliendo
all'equilibrio in una
soluzione preparata sciogliendo ![]() di acido formico e
di acido formico e
![]() di formiato di sodio in acqua, e portando il volume
della soluzione a
di formiato di sodio in acqua, e portando il volume
della soluzione a ![]() .
.
La costante di ionizzazione acida dell'acido formico e'
![]() .
.
Dati:
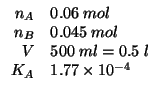
In seguito alla dissociazione completa del formiato sodico, si forma una quantita' corrispondente di ione formiato. La soluzione contiene dunque un acido debole (l'acido formico) e la sua base coniugata: si tratta quindi di una soluzione tampone.
La formula ricavata durante il corso per il calcolo del ![]() di una
soluzione tampone costituita da un acido debole e dalla sua base
coniugata e':
di una
soluzione tampone costituita da un acido debole e dalla sua base
coniugata e':
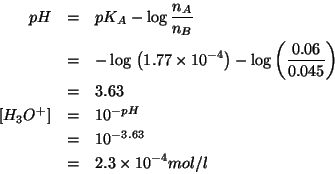
Notate che il dato del volume non era necessario.
La reazione:
ha un
![]() molto vicino a zero. Disegnate le strutture
di Lewis dei quattro composti e spiegate perche' e' ragionevole
aspettarsi che il
molto vicino a zero. Disegnate le strutture
di Lewis dei quattro composti e spiegate perche' e' ragionevole
aspettarsi che il
![]() sia cosi' piccolo.
sia cosi' piccolo.
Dati:
![]()
Applicando il procedimento appreso durante il corso per la scrittura delle formule di Lewis si ha:
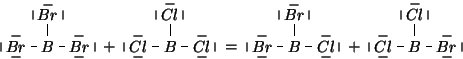
Si vede come nella reazione un legame ![]() e uno
e uno ![]() si
spezzano nei reagenti, ma si riformano nei prodotti (anche se su molecole
diverse). Siccome la variazione di entalpia e' data in prima
approssimazione dal bilancio energetico fra la rottura e la formazione
dei legami chimici, e' ragionevole aspettarsi che in questa reazione
il
si
spezzano nei reagenti, ma si riformano nei prodotti (anche se su molecole
diverse). Siccome la variazione di entalpia e' data in prima
approssimazione dal bilancio energetico fra la rottura e la formazione
dei legami chimici, e' ragionevole aspettarsi che in questa reazione
il ![]() sia molto piccolo.
sia molto piccolo.
L'acido nitroso ![]() disproporziona in soluzione acida
trasformandosi in ione nitrato
disproporziona in soluzione acida
trasformandosi in ione nitrato ![]() e monossido di azoto
e monossido di azoto
![]() . Scrivete e bilanciate l'equazione che descrive questa
reazione.
. Scrivete e bilanciate l'equazione che descrive questa
reazione.
L'equazione non bilanciata e':
Le coppie redox coinvolte sono: ![]() (ossidazione) e
(ossidazione) e
![]() (riduzione).
(riduzione).
Applicando il procedimento appreso durante il corso: