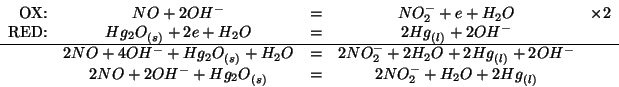 di
di 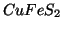
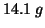 di
di
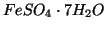
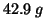 di
di
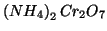
Dati:
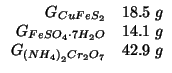
Altri simboli:
|
|
massa molare di |
|
|
massa molare di
|
|
|
massa molare di
|
| numero di moli di |
|
|
|
numero di moli di
|
|
|
numero di moli di
|
Direttamente dalla definizione di massa molare:
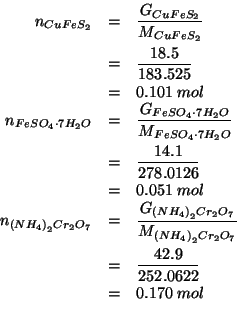
Altri simboli:
|
|
massa molare di
|
| massa molare di |
|
| massa molare di |
|
| massa molare di |
![]() del sale idrato (cioe'
del sale idrato (cioe' ![]() ) contiene
) contiene ![]() di
di ![]() (cioe'
(cioe' ![]() ). Quindi:
). Quindi:
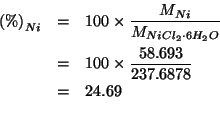
![]() del sale idrato (cioe'
del sale idrato (cioe' ![]() ) contiene
) contiene ![]() di
di ![]() (cioe'
(cioe'
![]() ). Quindi:
). Quindi:
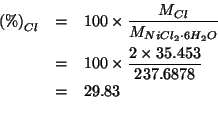
![]() del sale idrato (cioe'
del sale idrato (cioe' ![]() ) contiene
) contiene ![]() di
di ![]() (cioe'
(cioe'
![]() ). Quindi:
). Quindi:
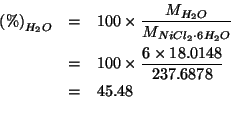
Ovviamente, la percentuale di acqua si poteva ottenere come
complemento a ![]() :
:
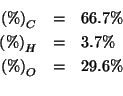
Dati:

Altri simboli:
| massa molare di |
|
| massa molare di |
|
| massa molare di |
|
| numero di moli di |
|
| numero di moli di |
|
| numero di moli di |
![]() del composto conterranno i seguenti numeri di moli dei tre
elementi costituenti:
del composto conterranno i seguenti numeri di moli dei tre
elementi costituenti:
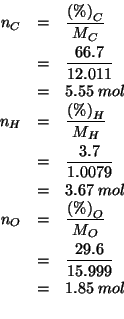
Gli indici dei tre elementi costituenti nella formula minima devono stare nello stesso rapporto dei numeri di moli appena trovati. Quindi:
La formula minima cercata e':
Applicando il semplice schema visto durante il corso per prevedere la sequenza energetica degli orbitali atomici si ottiene immediatamente:
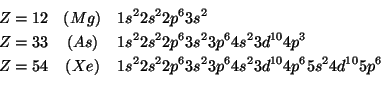
La formula del pentafluoruro di arsenico e' ![]() .
.
Per determinare la geometria molecolare cominciamo con lo scrivere la formula di Lewis della molecola.
| Elettroni di valenza | |
| carica | 0 |
| totale | |
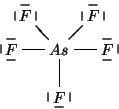
Si puo' facilmente verificare che questa e' la formula di risonanza piu' stabile. Tuttavia, la particolare formula di risonanza che si considera (purche' corretta!) non ha importanza, poiche' siamo interessati alla geometria molecolare e all'ibridazione dell'atomo centrale, che non dipendono dalla particolare formula di risonanza considerata.
Dalla formula di Lewis si ricava subito che il numero di coppie
strutturali e' ![]() . Da cio' segue che la geometria delle coppie
strutturali e' bipiramidale trigonale. Siccome non ci sono coppie di
non legame, la geometria molecolare coincidera' con quella delle
coppie strutturali.
. Da cio' segue che la geometria delle coppie
strutturali e' bipiramidale trigonale. Siccome non ci sono coppie di
non legame, la geometria molecolare coincidera' con quella delle
coppie strutturali.
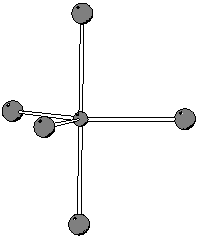
Infine, essendo la geometria delle coppie strutturali bipiramidale
trigonale, si prevede che l'atomo di arsenico presentera'
un'ibridazione di tipo ![]() .
.
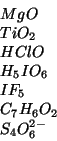
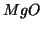 :
:- Quando e' legato a un elemento diverso dal fluoro,
l'ossigeno ha (quasi) sempre numero di ossidazione pari
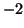 e
quindi il
e
quindi il 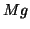 ha numero di ossidazione pari a
ha numero di ossidazione pari a 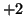 (questo
segue anche dal fatto che il
(questo
segue anche dal fatto che il 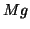 appartiene al secondo gruppo
della tavola periodica).
appartiene al secondo gruppo
della tavola periodica).
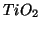 :
:- Analogamente al caso precedente:
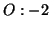 e, quindi,
e, quindi,
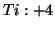 .
.
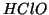 :
:- Assegnando all'idrogeno il numero di ossidazione
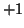 , all'ossigeno
, all'ossigeno 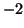 , per il cloro si ricava
, per il cloro si ricava 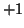 .
.
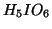 :
:- assegnando
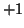 all'atomo di idrogeno e
all'atomo di idrogeno e 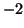 all'atomo di ossigeno, per lo iodio si ha
all'atomo di ossigeno, per lo iodio si ha
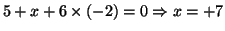 .
.
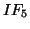 :
:- il fluoro ha numero di ossidazione pari a
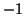 in
tutti i suoi composti, quindi, per lo iodio, si ottiene
in
tutti i suoi composti, quindi, per lo iodio, si ottiene 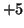 .
.
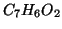 :
:- idrogeno e ossigeno hanno numero di ossidazione
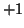 e
e 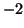 , rispettivamente. Per il carbonio si ottiene:
, rispettivamente. Per il carbonio si ottiene:
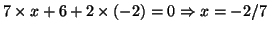 .
.
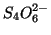 :
:- assegnando
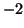 all'ossigeno, per lo zolfo
si ricava
all'ossigeno, per lo zolfo
si ricava
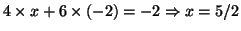 .
.
Applicando il metodo di bilanciamento appreso durante il corso si ha:
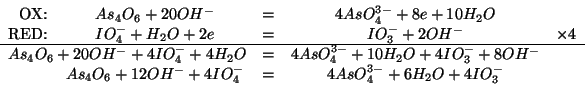
Dati:
![]()
Altri simboli:
|
|
massa molare di |
| massa molare di |
|
| numero di moli di |
|
| numero di moli di |
Dalla reazione bilanciata:
si ricava immediatamente il rapporto stechiometrico che lega le moli
di ![]() a quelle di
a quelle di ![]() :
: ![]() .
.
Quindi:
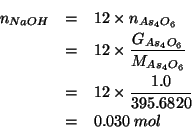
Infine, per avere la massa in grammi:
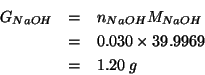
Dati:
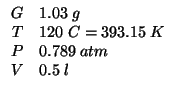
Altri simboli:
| costante dei gas:
|
|
| numero di moli della sostanza |
L'applicazione della legge dei gas ideali combinata con la definizione di massa molare fornisce:
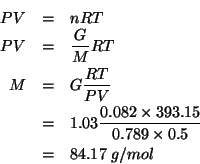
Dati:
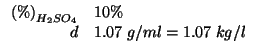
Altri simboli:
|
|
massa molare di |
| massa molare di |
|
| numero di moli di |
|
| numero di moli di |
|
| massa in grammi di |
|
| massa in grammi di |
|
| volume della soluzione in |
Per calcolare la molarita' ![]() , dobbiamo sapere quante moli di
, dobbiamo sapere quante moli di ![]() sono contenute in
sono contenute in ![]() della soluzione. La massa in grammi
della soluzione. La massa in grammi ![]() di
di ![]() di soluzione si ricava immediatamente a partire dalla densita':
di soluzione si ricava immediatamente a partire dalla densita':
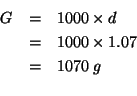
La massa di ![]() contenuta in un litro di soluzione sara',
pertanto:
contenuta in un litro di soluzione sara',
pertanto:
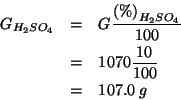
Questa massa corrisponde a:
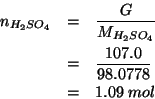
La molarita' e' dunque ![]() .
.
Per trovare la molalita' dobbiamo determinare quante moli di
![]() ci sono per chilogrammo di solvente puro (in questo caso
acqua).
ci sono per chilogrammo di solvente puro (in questo caso
acqua).
Consideriamo ![]() di soluzione. La massa in grammi di acido
solforico contenuta in questa massa di soluzione e' data da:
di soluzione. La massa in grammi di acido
solforico contenuta in questa massa di soluzione e' data da:
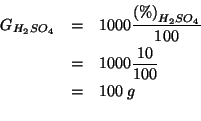
che, trasformata nel corrispondente numero di moli, diventa:
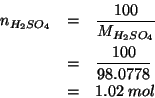
La massa di acqua in cui sono sciolte queste moli di acido e' ovviamente:

Quindi, la molalita' ![]() si ottiene nel modo seguente (notate la
trasformazione della massa di acqua in
si ottiene nel modo seguente (notate la
trasformazione della massa di acqua in ![]() ):
):
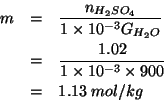
La massa ![]() di acido solforico per
di acido solforico per ![]() di solvente si ottiene
immediatamente dai dati gia' trovati:
di solvente si ottiene
immediatamente dai dati gia' trovati:
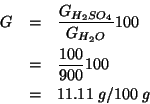
Infine, dalla definizione di frazione molare:
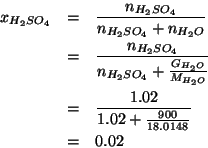
Dati:
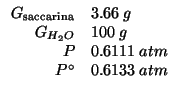
Altri simboli:
|
|
numero di moli di saccarina |
| numero di moli di acqua | |
|
|
massa molare della saccarina |
| massa molare dell'acqua:
|
|
| frazione molare dell'acqua |
L'applicazione della legge di Raoult fornisce:
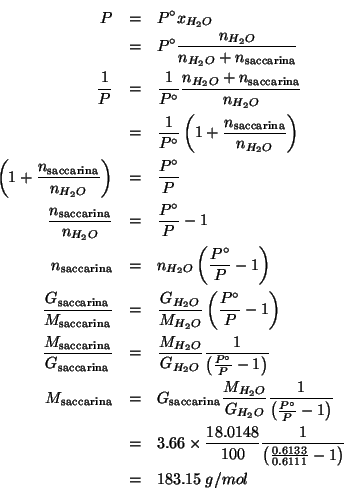
Dati:
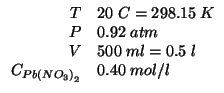
Altri simboli:
| numero di moli di |
|
|
|
numero di moli di
|
| costante dei gas:
|
Innanzitutto, dalla reazione bilanciata si ricava immediatamente che
il numero di moli di ![]() necessario dovra' essere doppio di quello
di
necessario dovra' essere doppio di quello
di
![]() :
:
D'altro canto,
![]() si ottiene dalla
concentrazione e dal volume della soluzione:
si ottiene dalla
concentrazione e dal volume della soluzione:
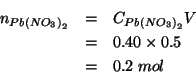
Combinando questo con l'equazione ![]() si ottiene:
si ottiene:
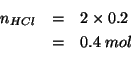
Infine, il volume occupato da ![]() di
di ![]() gassoso nelle
condizioni date si ricava applicando la legge dei gas ideali:
gassoso nelle
condizioni date si ricava applicando la legge dei gas ideali:
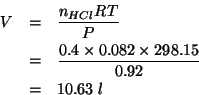
Dati:
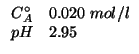
L'espressione che da' la concentrazione di ioni idronio in una soluzione contenente un acido debole di data concentrazione e':
Il testo del problema fornisce ![]() e il
e il ![]() della
soluzione, da cui e' immediato ricavarsi
della
soluzione, da cui e' immediato ricavarsi ![]() . Quindi:
. Quindi:
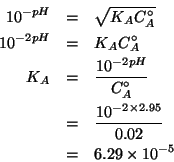
Dati:
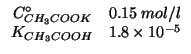
Altri simboli:
| costante di autoionizzazione dell'acqua:
|
|
|
|
costante di ionizzazione basica dello ione acetato |
L'acetato di potassio (![]() ) e' un sale e come tale si
dissocia completamente dando concentrazioni stechiometriche di ioni
acetato e ioni potassio. Gli ioni potassio hanno caratteristiche
acido-base trascurabili, mentre gli ioni acetato daranno idrolisi
basica, secondo:
) e' un sale e come tale si
dissocia completamente dando concentrazioni stechiometriche di ioni
acetato e ioni potassio. Gli ioni potassio hanno caratteristiche
acido-base trascurabili, mentre gli ioni acetato daranno idrolisi
basica, secondo:
In pratica, il problema e' quello di trovare il ![]() di una
soluzione contenente una base debole (lo ione acetato) in
concentrazione pari a
di una
soluzione contenente una base debole (lo ione acetato) in
concentrazione pari a ![]() . La relazione che fornisce la
concentrazione di ioni
. La relazione che fornisce la
concentrazione di ioni ![]() per tale soluzione e':
per tale soluzione e':
Chiaramente,
![]() si ottiene immediatamente sapendo che:
si ottiene immediatamente sapendo che:
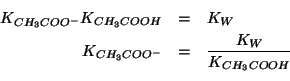
Quindi:
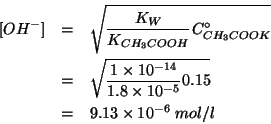
Infine, per ottenere il ![]() :
:
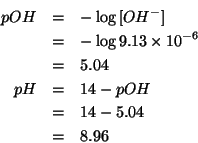
Dati:
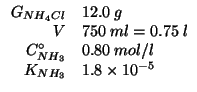
Altri simboli:
| massa molare di |
|
| numero di moli di ammoniaca | |
| numero di moli di ione ammonio |
Il cloruro d'ammonio, come tutti i sali, e' un elettrolita forte e
quindi si dissocia completamente in ioni ammonio e cloruro. La
soluzione finale contiene dunque entrambi i membri della coppia
coniugata ![]() : si tratta cioe' di una soluzione
tampone. Il
: si tratta cioe' di una soluzione
tampone. Il ![]() di tale soluzione tampone e' dato da:
di tale soluzione tampone e' dato da:
Il numero di moli di ammoniaca si ottiene conoscendo il volume e la concentrazione della soluzione:

Il numero di moli di ione ammonio (ovviamente identico al numero di moli di sale) si ottiene dalla definizione di massa molare:
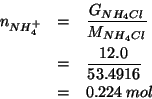
Quindi:
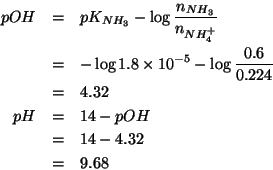
Dati:
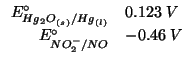
Dall'esame dei potenziali standard e' evidente che l'equazione da bilanciare e':
corrispondente, cioe', alla riduzione dell'ossido di mercurio e all'ossidazione del monossido di azoto.
Applicando il metodo visto durante il corso si ha: