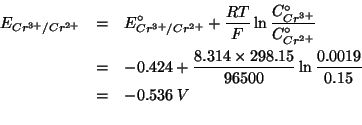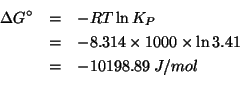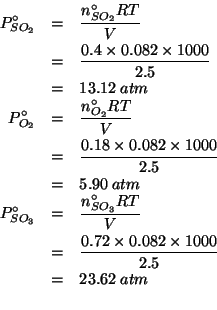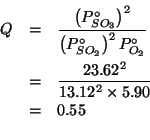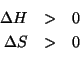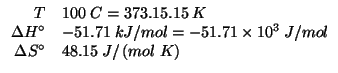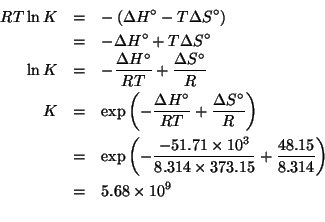Dati:
Altri simboli:
|
|
abbondanza percentuale del secondo isotopo |
Durante il corso abbiamo visto come la massa atomica di un dato
elemento sia la media delle masse atomiche dei suoi isotopi.
Quindi, tenendo presente che l'abbondanza percentuale del secondo
isotopo e' semplicemente il complemento a ![]() dell'abbondanza
percentuale del primo (visto che ce ne sono solo due):
dell'abbondanza
percentuale del primo (visto che ce ne sono solo due):
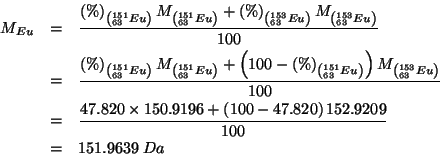
- quante moli
- quante molecole
sono presenti in ![]() di acetato di
isoamile. (Questo esercizio vale
di acetato di
isoamile. (Questo esercizio vale ![]() punto)
punto)
Dati:
![]()
Altri simboli:
|
|
massa molare di |
| numero di Avogadro:
|
|
| numero di moli di |
|
| numero di molecole di |
Dalla definizione di massa molare:
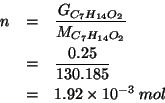
Dalla definizione di numero di Avogadro:
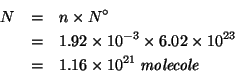
Dati:
![]()
Altri simboli:
| massa molare di |
|
| massa molare di |
|
| numero di moli di |
|
| numero di moli di |
La formula chimica di ![]() dice immediatamente che:
dice immediatamente che:
Quindi, la massa in grammi di ![]() e' ottenuta da:
e' ottenuta da:
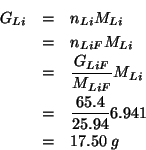
Dati:
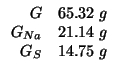
Altri simboli:
| massa di ossigeno in |
|
| massa molare di |
|
| massa molare di |
|
| massa molare di |
|
| numero di moli di |
|
| numero di moli di |
|
| numero di moli di |
Innanzitutto, la massa di ossigeno si ricava immediatamente per differenza:
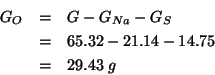
Ora trasformiamo le masse nei corrispondenti numeri di moli:
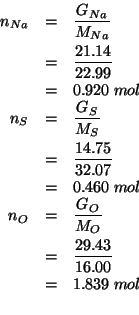
I numeri di moli cosi' ottenuti devono stare nello stesso rapporto in cui stanno gli indici dei tre elementi nella formula minima del composto. Dividendo per il piu' piccolo di essi si ottiene:
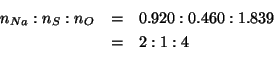
La formula minima cercata e':
Si pongono a reagire ![]() di
di ![]() con
con ![]() di
di
![]() . Calcolate le masse in grammi di tutti i partecipanti alla
reazione dopo che questa e' avvenuta. Assumete che la reazione sia
completa. (Questo esercizio vale
. Calcolate le masse in grammi di tutti i partecipanti alla
reazione dopo che questa e' avvenuta. Assumete che la reazione sia
completa. (Questo esercizio vale ![]() punti)
punti)
Dati:
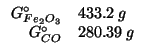
Altri simboli:
| massa di |
|
| massa di |
|
| massa di |
|
| massa di |
|
|
|
massa molare di |
| massa molare di |
|
| massa molare di |
|
| massa molare di |
|
|
|
numero di moli iniziale di |
| numero di moli iniziale di |
|
| numero di moli finale di |
|
| numero di moli finale di |
|
| numero di moli finale di |
|
| numero di moli finale di |
Prima di tutto trasformiamo le masse dei reagenti nei corrispondenti
numeri di moli:
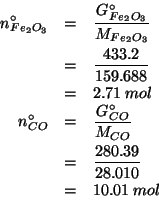
Ora rappresentiamo la reazione con la seguente tabella:
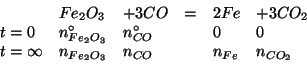
Il problema consiste nel trovare i numeri di moli a fine reazione ( e trasformarli poi nelle corrispondenti masse in grammi).
Siccome la reazione e' completa, dobbiamo individuare il reagente limitante. A tale scopo basta dividere il numero di moli iniziale dei due reagenti per il rispettivo coefficiente stechiometrico:
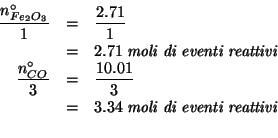
Dal confronto si deduce subito che il reagente limitante e' il
![]() . Quindi, si trova subito che dovra' essere:
. Quindi, si trova subito che dovra' essere:
![]() .
.
Sapendo che ![]() verra' consumato completamente e basandosi
sulla stechiometria della reazione, si ricavano immediatamente tutti
gli altri numeri di moli finali:
verra' consumato completamente e basandosi
sulla stechiometria della reazione, si ricavano immediatamente tutti
gli altri numeri di moli finali:
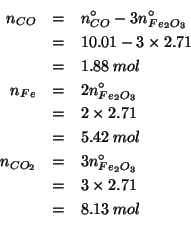
In definitiva:
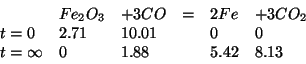
Non resta che trasformare le moli in grammi:
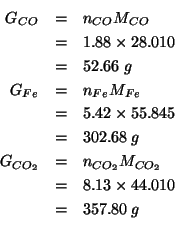
Per verificare la correttezza del risultato ottenuto, si puo' verificare che la massa totale e' conservata:
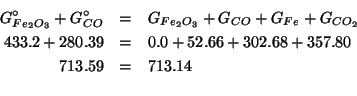
Le due masse totali (quella prima e quella dopo la reazione) sono in
accordo entro lo ![]() : la piccola differenza e' senz'altro
dovuta alle approssimazioni dei calcoli.
: la piccola differenza e' senz'altro
dovuta alle approssimazioni dei calcoli.
![\begin{displaymath}
\begin{array}{cc}
\left[
\begin{xy}
<1em,0em>:
c*+{O};p=''O...
...,
\end{xy}\right]^-
\\
&\\
(c)~SbF_3&(d)~SCN^-\\
\end{array}\end{displaymath}](img90.gif)
(Questo esercizio vale ![]() punti)
punti)
Applicando il metodo visto durante il corso per il calcolo della
carica atomica formale, ogni atomo di ossigeno viene ad essere
circondato da ![]() elettroni, mentre l'atomo centrale di zolfo
risulta circondato da
elettroni, mentre l'atomo centrale di zolfo
risulta circondato da ![]() elettroni.
elettroni.
![\begin{displaymath}
\left[
\begin{xy}
<1em,0em>:
c*+{O};p=''O'';
''O'';
p+/u0.1...
...\vert},
p+/r0.1em/**\dir{}?<*\dir{\vert};
\end{xy}\right]^{2-}
\end{displaymath}](img93.gif)
Quindi, ogni atomo di ossigeno nella formula di Lewis possiede ![]() elettrone in piu' rispetto ad un atomo di ossigeno isolato e percio' ha
carica atomica formale pari a
elettrone in piu' rispetto ad un atomo di ossigeno isolato e percio' ha
carica atomica formale pari a ![]() . Analogamente, l'atomo di zolfo
nella formula di Lewis possiede
. Analogamente, l'atomo di zolfo
nella formula di Lewis possiede ![]() elettroni in meno rispetto
ad un atomo di zolfo isolato e percio' la sua carica atomica formale
e'
elettroni in meno rispetto
ad un atomo di zolfo isolato e percio' la sua carica atomica formale
e' ![]() .
.
In questo caso si ha:
![\begin{displaymath}
\left[
\begin{xy}
<1em,0em>:
c*+{O};p=''O'';
''O'';
p+/u0.1...
...\vert},
p+/r0.1em/**\dir{}?<*\dir{\vert};
\end{xy}\right]^{2-}
\end{displaymath}](img93.gif)
Gli atomi di ossigeno si trovano esattamente nelle stesse condizioni
del caso precedente, per cui hanno carica atomica formale pari a
![]() . Anche per lo zolfo centrale la situazione e' identica a quella
del caso (a), per cui la sua carica atomica formale e' pari a
. Anche per lo zolfo centrale la situazione e' identica a quella
del caso (a), per cui la sua carica atomica formale e' pari a
![]() . La carica atomica dell'atomo di zolfo terminale si puo'
ricavare osservando che la somma delle cariche atomiche formali deve
essere uguale alla carica risultante dello ione:
. La carica atomica dell'atomo di zolfo terminale si puo'
ricavare osservando che la somma delle cariche atomiche formali deve
essere uguale alla carica risultante dello ione:
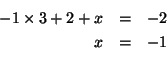
Alternativamente, si puo' osservare che l'atomo di zolfo terminale e'
circondato da ![]() elettroni: avendo
elettroni: avendo ![]() elettrone in piu'
rispetto ad un atomo di zolfo isolato, la sua carica atomica formale
e' pari a
elettrone in piu'
rispetto ad un atomo di zolfo isolato, la sua carica atomica formale
e' pari a ![]() .
.
In questo caso si ha:
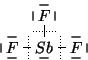
Ogni atomo di fluoro della formula di Lewis e' circondato da ![]() elettroni: avendo lo stesso numero di elettroni di un atomo di fluoro
isolato, la carica atomica formale di ciscun atomo di fluoro e'
elettroni: avendo lo stesso numero di elettroni di un atomo di fluoro
isolato, la carica atomica formale di ciscun atomo di fluoro e' ![]() .
.
L'atomo di antimonio centrale e' circondato da ![]() elettroni e
quindi, avendo lo stesso numero di elettroni di un atomo di antimonio
isolato, ha carica atomica formale
elettroni e
quindi, avendo lo stesso numero di elettroni di un atomo di antimonio
isolato, ha carica atomica formale ![]() . Questo si poteva dedurre
subito dal fatto che gli atomi di fluoro hanno carica nulla e che la
molecola del trifluoruro di antimonio e' elettricamente neutra.
. Questo si poteva dedurre
subito dal fatto che gli atomi di fluoro hanno carica nulla e che la
molecola del trifluoruro di antimonio e' elettricamente neutra.
In questo caso si ha:
L'atomo di zolfo e' circondato da ![]() elettroni,
elettroni, ![]() in
piu' rispetto ad un atomo di zolfo isolato: la sua carica atomica
formale e' quindi
in
piu' rispetto ad un atomo di zolfo isolato: la sua carica atomica
formale e' quindi ![]() .
.
L'atomo di azoto e' circondato da ![]() elettroni, esattamente come un
atomo di azoto isolato: la sua carica atomica formale e' percio'
elettroni, esattamente come un
atomo di azoto isolato: la sua carica atomica formale e' percio'
![]() .
.
La carica atomica formale dell'atomo di carbonio si puo' ricavare dalla relazione:
oppure osservando che l'atomo di carbonio e' circondato da
![]() elettroni, esattamente come un atomo di carbonio isolato.
elettroni, esattamente come un atomo di carbonio isolato.
Cominciamo col determinare il numero totale di elettroni di valenza:
| Elettroni di valenza | |
| carica | 0 |
| totale | |
Ora iniziamo a disegnare lo scheletro ![]() della molecola,
secondo le indicazioni del testo dell'esercizio:
della molecola,
secondo le indicazioni del testo dell'esercizio:
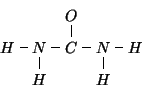
Lo schema finora disegnato ha impegnato ![]() coppie di elettroni, per
cui ne rimangono
coppie di elettroni, per
cui ne rimangono ![]() da ``sistemare''. Le useremo per completare gli
ottetti attorno agli atomi terminali (escludendo, ovviamente, gli
atomi di idrogeno). Si ottiene:
da ``sistemare''. Le useremo per completare gli
ottetti attorno agli atomi terminali (escludendo, ovviamente, gli
atomi di idrogeno). Si ottiene:
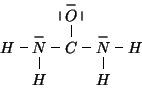
Nella formula di Lewis cosi' ottenuta, l'atomo di carbonio centrale non e'
circondato da ![]() elettroni: dovremo percio' utilizzare un doppietto
di non legame di un atomo terminale per formare un legame
elettroni: dovremo percio' utilizzare un doppietto
di non legame di un atomo terminale per formare un legame ![]() con
l'atomo centrale.
con
l'atomo centrale.
Ci sono in teoria due possibilita':
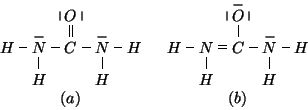
(la formula (b) ha una ``gemella'' in cui il legame ![]() si forma fra l'atomo di carbonio e l'atomo di azoto alla sua destra)
si forma fra l'atomo di carbonio e l'atomo di azoto alla sua destra)
Per stabilire quale delle due strutture e' la piu' stabile, dobbiamo valutare la carica atomica formale degli atomi in ciascuna di esse.
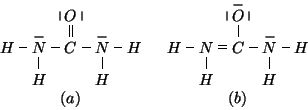
Valutando il numero di elettroni di ciascun atomo nella formula di Lewis e confrontandolo con il numero di elettroni di un atomo dello stesso tipo isolato, si ricavano facilmente le cariche atomiche formali degli atomi nelle due formule limite:
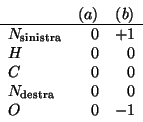
E' quindi evidente che la formula di Lewis piu' stabile e' la ![]() .
.
- Individuate le coppie redox coinvolte nella reazione e indicate lo stato di ossidazione della forma ridotta e ossidata di ciascuna coppia.
- Indicate quale coppia reagisce nel verso della riduzione e quale in quello dell'ossidazione.
- Verificate che il numero totale di elettroni persi nell'ossidazione e' uguale a quello degli elettroni acquistati nella riduzione.
(Questo esercizio vale ![]() punti)
punti)
Le coppie redox coinvolte nella reazione sono:
Con il metodo appreso durante il corso si ottengono gli stati di ossidazione dell'arsenico e dello iodio:

Dall'analisi dei numeri di ossidazione si deduce subito che la coppia
redox
![]() reagisce nel verso dell'ossidazione mentre
la coppia
reagisce nel verso dell'ossidazione mentre
la coppia ![]() reagisce nel verso della riduzione.
reagisce nel verso della riduzione.
Osservando l'equazione bilanciata e tenendo presente le variazioni
del numero di ossidazione, ciascun atomo di arsenico passa da un numero
di ossidazione ![]() a un numero di ossidazione
a un numero di ossidazione ![]() : in totale,
quindi, l'ossidazione ``produce'':
: in totale,
quindi, l'ossidazione ``produce'': ![]() elettroni.
elettroni.
Ciascun atomo di iodio passa da un numero di ossidazione ![]() a un
numero di ossidazione
a un
numero di ossidazione ![]() : in totale, la riduzione ``consuma'':
: in totale, la riduzione ``consuma'':
![]() elettroni.
elettroni.
Dati:
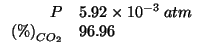
Altri simboli:
| numero di moli di |
|
| numero di moli di |
|
| massa di |
|
| massa di |
|
| massa molare di |
|
| massa molare di |
Consideriamo per comodita' una massa pari a ![]() dell'atmosefra
di Marte. In tale massa saranno contenuti i seguenti numeri di moli
dei due principali componenti:
dell'atmosefra
di Marte. In tale massa saranno contenuti i seguenti numeri di moli
dei due principali componenti:
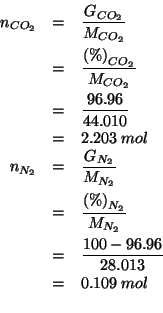
La frazione molare di ![]() e' presto calcolata:
e' presto calcolata:
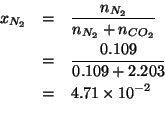
Infine, la pressione parziale si ricava dalla pressione totale e dalla frazione molare:
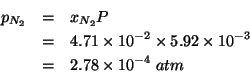
| Punto triplo | 0.123 | 63.15 |
| Punto critico | 33.40 | 126.19 |
| Temperatura normale di ebollizione | 1.0 | 77.35 |
| Temperatura normale di fusione | 1.0 | 63.29 |
Usate questi dati per disegnare il diagramma di stato dell'azoto (non
e' assolutamente necessario che i punti caratteristici del diagramma
siano in scala!). La densita' media dell'azoto solido e'
![]() , quella dell'azoto liquido e'
, quella dell'azoto liquido e'
![]() .
.
(Questo esercizio vale ![]() punti)
punti)
Dati:

Sulla base dei dati disponibili, il diagramma di stato dell'azoto (non in scala) risulta:
![\begin{psfrags}\psfrag{P} [r][r]{{$P$}}\psfrag{PC} [r][r]{{$P_C$}}\psfrag{...
...}\psfrag{TC} [c][c]{{$T_C$}}
\includegraphics{state-diag-N2.eps}
\end{psfrags}](img145.gif)
Notate che, essendo:
la pendenza della curva di equilibrio
![]() e' positiva.
e' positiva.
Dati:
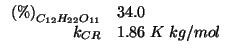
Altri simboli:
|
|
massa molare di
|
| massa molare di |
|
|
|
numero di moli di
|
| numero di moli di |
|
|
|
massa di
|
| massa di |
Per comodita', consideriamo ![]() della miscela, che conterranno
quindi
della miscela, che conterranno
quindi ![]() di saccarosio e
di saccarosio e
![]() di acqua.
di acqua.
Possiamo immediatamente ricavare la molalita' del saccarosio. Dalla definizione:
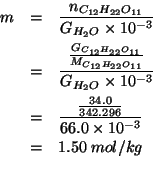
Avendo la molalita', possiamo ottenere l'abbassamento crioscopico:
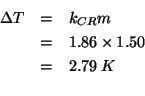
Infine, sapendo che l'acqua pura congela a ![]() , possiamo dire che
il primo gelato comparira' nel recipiente quando la temperatura avra'
raggiunto il valore di
, possiamo dire che
il primo gelato comparira' nel recipiente quando la temperatura avra'
raggiunto il valore di ![]() (
(![]() ).
).
e': ![]() .
.
Calcolate la costante di equilibrio a ![]() per la reazione:
per la reazione:
(Questo esercizio vale ![]() punti)
punti)
Dati:
![]()
E' facile rendersi conto che la reazione di cui si deve trovare la
costante di equilibrio e' l'inversa della prima reazione, in cui,
inoltre, tutti i coefficienti stechiometrici sono stati moltiplicati
per ![]() . Sulla base delle proprieta' della costante di equilibrio
apprese durante il corso, si deduce immediatamente che la costante
cercata si ricava dalla costante data nel modo seguente:
. Sulla base delle proprieta' della costante di equilibrio
apprese durante il corso, si deduce immediatamente che la costante
cercata si ricava dalla costante data nel modo seguente:
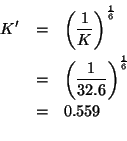

(Questo esercizio vale ![]() punti)
punti)
Altri simboli:
| costante di ionizzazione acida di |
|
| costante di ionizzazione acida di |
E' facile realizzare che la reazione data si puo' scomporre nel modo seguente:
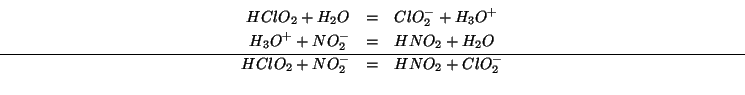
La prima delle due reazioni componenti e' semplicemente la ionizzazione dell'acido cloroso, la cui costante si ricava dalla tabella data; la seconda e' l'inversa della ionizzazione dell'acido nitroso: la sua costante di equilibrio e' l'inverso della costante di ionizzazione dell'acido nitroso, anch'essa presente nella tabella.
Quindi, detta ![]() la costante di equilibrio cercata, sara':
la costante di equilibrio cercata, sara':
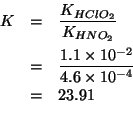
Il valore della costante di ionizzazione dell'acido sulfanilico e'
![]() .
.
![]() di acido sulfanilico e
di acido sulfanilico e ![]() di sulfanilato di
sodio (
di sulfanilato di
sodio (
![]() ) sono sciolte in acqua e diluite a
) sono sciolte in acqua e diluite a
![]() per preparare un tampone.
per preparare un tampone.
- Calcolate il
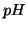 della soluzione
della soluzione
- Supponete che
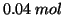 di
di 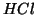 siano aggiunte al
tampone. Qual'e' il
siano aggiunte al
tampone. Qual'e' il 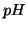 dopo l'aggiunta dell'acido cloridrico?
dopo l'aggiunta dell'acido cloridrico?
(Questo esercizio vale ![]() punti)
punti)
Dati:
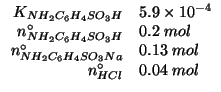
Il ![]() della soluzione tampone appena preparata si puo' calcolare
applicando l'espressione ricavata durante il corso:
della soluzione tampone appena preparata si puo' calcolare
applicando l'espressione ricavata durante il corso:
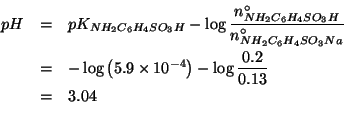
L'aggiunta dell'acido forte viene neutralizzata dal tampone con la seguente reazione:
Come si e' visto durante il corso, questa reazione e' praticamente completa (la sua costante di equilibrio e' l'inverso della costante di ionizzazione dell'acido sulfanilico). Quindi, considerando la reazione completa e osservando che il reagente limitante e' l'acido cloridrico, si ha:
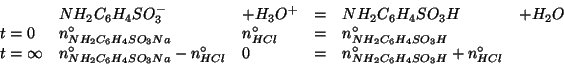
I valori finale delle concentrazioni dell'acido sulfanilico e della
sua base coniugata possono essere reinseriti nell'espressione usata al
punto (a) per ottenere il ![]() dopo l'aggiunta dell'acido
cloridrico:
dopo l'aggiunta dell'acido
cloridrico:
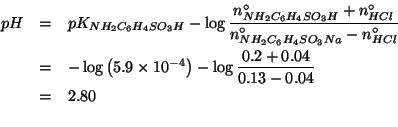
Notate come il ![]() sia diminuito: risultato ragionevole, dato che
e' stato aggiunto un acido forte. D'altro canto, la diminuzione e'
piuttosto contenuta: questo e' l'effetto tampone.
sia diminuito: risultato ragionevole, dato che
e' stato aggiunto un acido forte. D'altro canto, la diminuzione e'
piuttosto contenuta: questo e' l'effetto tampone.
(Questo esercizio vale ![]() punti)
punti)
Si vede subito che la reazione e' una disproporzione: infatti, la
presenza di ![]() elementare al secondo membro suggerisce che si
tratta di una reazione redox. Inoltre, al primo membro compare
un'unica specie, che quindi deve fare parte di entrambe le coppie redox
coinvolte. Queste ultime sono la coppia
elementare al secondo membro suggerisce che si
tratta di una reazione redox. Inoltre, al primo membro compare
un'unica specie, che quindi deve fare parte di entrambe le coppie redox
coinvolte. Queste ultime sono la coppia ![]() , che reagisce
nel verso della riduzione (il numero di ossidazione dello
, che reagisce
nel verso della riduzione (il numero di ossidazione dello ![]() passa
da
passa
da ![]() a
a ![]() ), e la coppia
), e la coppia
![]() , che reagisce
nel verso dell'ossoidazione (il numero di ossidazione dello
, che reagisce
nel verso dell'ossoidazione (il numero di ossidazione dello ![]() passa da
passa da ![]() a
a ![]() ).
).
Applicando il procedimento generale appreso durante il corso, si ottiene:
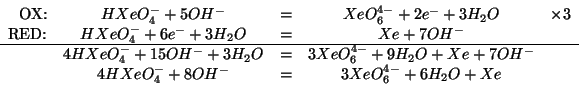
Dati:
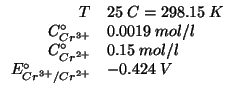
Altri simboli:
| costante dei gas:
|
|
| costante di Faraday: |
Come detto durante il corso, se i partecipanti ad una semireazione elettrodica non sono tutti in concentrazione unitaria, il potenziale elettrodico non ha il valore standard, ma deve essere calcolato con l'equazione di Nernst. Nel caso in esame, la semireazione elettrodica e':
e quindi: