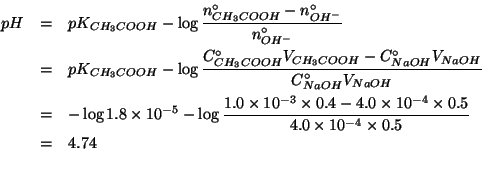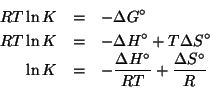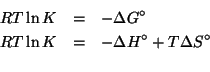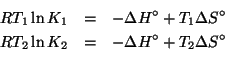Dati:
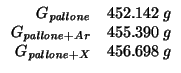
Altri simboli:
| costante dei gas:
|
|
| numero di moli del gas contenuto nel pallone | |
| pressione all'interno del pallone in |
|
| temperatura del pallone in |
|
| volume del pallone in |
|
| massa molare dell'argon: |
|
| massa di |
|
| massa della sostanza incognita in |
Consideriamo la legge dei gas ideali:
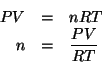
Siccome ![]()
![]() e
e ![]() sono costanti nei due casi, segue
immediatamente da quanto appena scritto che il numero di moli di
sono costanti nei due casi, segue
immediatamente da quanto appena scritto che il numero di moli di
![]() e della sostanza incognita e' lo stesso.
e della sostanza incognita e' lo stesso.
La massa molare della sostanza incognita e' data per definizione da:
Chiaramente:
Per trovare ![]() basta sfruttare i dati per l'argon:
basta sfruttare i dati per l'argon:
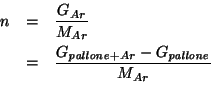
Non resta che sostituire:
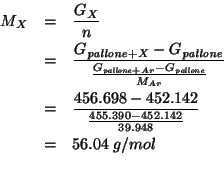
- (a)
- soluzione
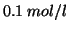 di
di
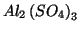
- (b)
- soluzione
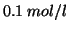 di zucchero (
di zucchero (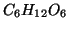 )
)
- (c)
- soluzione
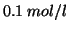 di
di 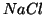
(Questo esercizio vale ![]() punti)
punti)
Dati:
![]()
Altri simboli:
|
|
concentrazione colligativa di
|
| concentrazione colligativa di |
|
|
|
concentrazione colligativa di |
![]() e
e ![]() sono dei sali e quindi si
dissociano completamente in soluzione acquosa. Lo zucchero, invece, e'
un tipico non elettrolita.
sono dei sali e quindi si
dissociano completamente in soluzione acquosa. Lo zucchero, invece, e'
un tipico non elettrolita.
Le equazioni che descrivono la dissociazione dei due sali sono:
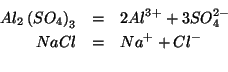
Si conclude quindi che le concentrazioni colligative (cioe' le concentrazioni da usare nella legge della pressione osmotica) sono:
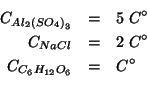
Essendo le molarita' formali delle tre soluzioni identiche, l'ordine crescente della loro pressione osmotica sara':
dove ![]() e' la costante di ionizzazione basica della
base debole,
e' la costante di ionizzazione basica della
base debole, ![]() la sua concentrazione iniziale e
la sua concentrazione iniziale e
![]() e' la concentrazione iniziale dell'acido
coniugato. Illustrate brevemente le approssimazioni che portano alla
formula su scritta. (Questo esercizio vale
e' la concentrazione iniziale dell'acido
coniugato. Illustrate brevemente le approssimazioni che portano alla
formula su scritta. (Questo esercizio vale ![]() punti)
punti)
Detta ![]() la base debole, essa sara' in equilibrio con il suo acido
coniugato secondo:
la base debole, essa sara' in equilibrio con il suo acido
coniugato secondo:
La costante di equilibrio della reazione rappresentata dall'equazione
su scritta e' la costante di ionizzazione basica della base debole
che, per definizione, e' molto piccola. A cio' va aggiunto che in una
soluzione tampone si trova gia' una concentrazione apprezzabile
dell'acido coniugato della base debole (![]() nel nostro
caso): in base a queste due considerazioni si puo' assumere, in prima
approssimazione, che la reazione su scritta in pratica non avvenga e
che, pertanto, le concentrazioni finali di equilibrio della base
debole e del suo acido coniugato coincidano con i loro valori iniziali
(
nel nostro
caso): in base a queste due considerazioni si puo' assumere, in prima
approssimazione, che la reazione su scritta in pratica non avvenga e
che, pertanto, le concentrazioni finali di equilibrio della base
debole e del suo acido coniugato coincidano con i loro valori iniziali
(![]() e
e ![]() , rispettivamente). Allora, la concentrazione di ioni ossidrile nel tampone puo' essere ricavata immediatamente sfruttando la legge dell'azione di massa per
, rispettivamente). Allora, la concentrazione di ioni ossidrile nel tampone puo' essere ricavata immediatamente sfruttando la legge dell'azione di massa per ![]() in cui vengono inseriti i due valori
approssimati delle concentrazioni di equilibrio della base debole e
del suo acido coniugato:
in cui vengono inseriti i due valori
approssimati delle concentrazioni di equilibrio della base debole e
del suo acido coniugato:
![\begin{eqnarray*}
K_B&=&\frac{\left[OH^-\right]C^\circ_A}{C^\circ_B}\\
\left[OH^-\right]&=&K_B\frac{C^\circ_B}{C^\circ_A}
\end{eqnarray*}](img45.gif)
La formula finale si ottiene prendendo la funzione ![]() di ambo i
membri:
di ambo i
membri:
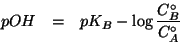
Dati:

Altri simboli:
| massa molare di |
|
| massa molare di |
|
| massa molare di |
|
| massa molare di |
|
| massa molare di |
|
| numero di moli di |
|
| numero di moli di |
|
| numero di moli di |
|
| numero di moli di |
|
| numero di moli di |
|
| massa di |
|
| massa di |
|
| massa di |
|
| numero di moli di |
|
| numero di moli di |
|
| numero di moli di |
Indicando con ![]() la sostanza incognita, l'equazione che
descrive la reazione di combustione e':
la sostanza incognita, l'equazione che
descrive la reazione di combustione e':
Osservate che non e' necessario conoscere il destino dell'azoto contenuto nella sostanza incognita, perche' la sua quantita' si ricava per differenza, come vedremo.
Dall'equazione appare evidente che:
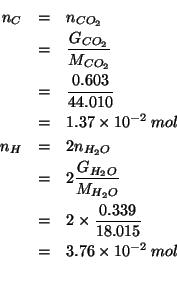
Le moli di azoto contenute nei ![]() di sostanza si ottengono con:
di sostanza si ottengono con:
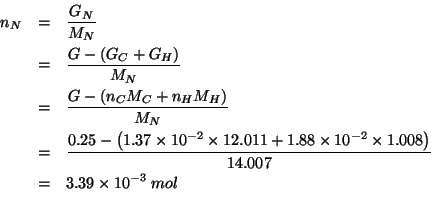
A questo punto osserviamo che il numero di moli di un dato elemento
in una sostanza e' ovviamente proporzionale alla massa di
sostanza. Quindi possiamo immediatamente trovare quante moli di ![]()
![]() e
e ![]() sono contenute in una massa molare della sostanza incognita:
sono contenute in una massa molare della sostanza incognita:
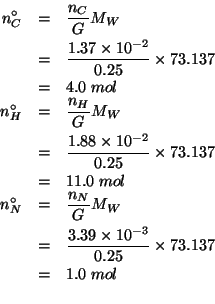
E' chiaro che i numeri di moli trovati coincidono con gli indici dei tre elementi nella formula molecolare, che quindi e':
Guardando la tavola periodica e applicando lo schema visto durante il corso per ricavare la configurazione elettronica dello stato fondamentale degli elementi:

si ricava che l'elemento appartenente al settimo periodo e al gruppo degli alogeni avrebbe la seguente configurazione:
per un totale di:
Questo, ovviamente, coincide con il numero atomico cercato.
Applicando il metodo visto durante il corso, scriviamo le formule di Lewis per le due strutture proposte. Il numero di elettroni di valenza totali e' ovviamente lo stesso in entrambi i casi:
| Elettroni di valenza | |
| carica | 0 |
| totale | |
Per la struttura con l'azoto centrale lo scheletro ![]() che si
ottiene e':
che si
ottiene e':
L'azoto non e' circondato da ![]() elettroni e quindi ci sono due
possibilita':
elettroni e quindi ci sono due
possibilita':
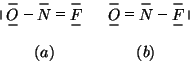
Le cariche atomiche formali sui tre atomi nelle due strutture limite sono:
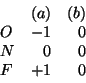
Per la struttura con l'ossigeno centrale lo scheletro ![]() che si
ottiene e':
che si
ottiene e':
L'ossigeno non e' circondato da ![]() elettroni e quindi ci sono due
possibilita':
elettroni e quindi ci sono due
possibilita':
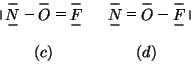
Le cariche atomiche formali sui tre atomi nelle due strutture limite sono:
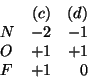
Come si vede, solo nella formula di Lewis (b) tutti gli atomi hanno
carica atomica formale pari a ![]() : tale struttura e' di gran lunga
la piu' stabile. Se ne conclude che nella molecola del composto
l'atomo centrale sara' l'azoto, e non l'ossigeno.
: tale struttura e' di gran lunga
la piu' stabile. Se ne conclude che nella molecola del composto
l'atomo centrale sara' l'azoto, e non l'ossigeno.
Per prima cosa valutiamo il numero totale di elettroni di valenza.
| Elettroni di valenza | |
| carica | |
| totale | |
Ora scriviamo lo schema ![]() ; l'atomo centrale e' ovviamente
quello di azoto:
; l'atomo centrale e' ovviamente
quello di azoto:
Il calcolo delle cariche atomiche formali e' immediato:
Queste cariche atomiche formali sono le piu' piccole possibile,
compatibilmente con il fatto che lo ione ha una carica elettrica
risultante pari a ![]() . La formula di Lewis su scritta e' quindi la
piu' stabile (in realta' e' anche l'unica che si puo' scrivere).
. La formula di Lewis su scritta e' quindi la
piu' stabile (in realta' e' anche l'unica che si puo' scrivere).
Basandosi sulla formula di Lewis, e' facile prevedere la geometria molecolare con il modello VSEPR:
| coppie strutturali | 4 |
| geometria delle coppie strutturali | tetraedrica |
| modello |
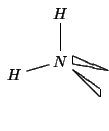 |
| coppie di non legame | 2 |
| geometria molecolare | angolata |
Infine, dal fatto che la geometria delle coppie strutturali e'
tetraedrica, si deduce che l'ibridazione dell'atomo di azoto dovra'
essere di tipo ![]() .
.
Dati:
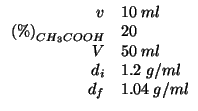
Altri simboli:
|
|
massa molare di |
| massa molare di |
|
|
|
numero di moli di |
| numero di moli di |
|
| massa della soluzione di partenza in |
|
| massa di |
|
| massa della soluzione finale in |
|
| massa di |
Calcoliamo il numero di moli di ![]() contenuto nella soluzione
di partenza:
contenuto nella soluzione
di partenza:
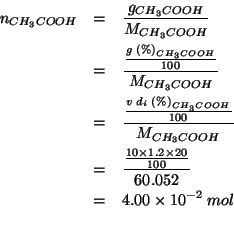
Ovviamente, questo e' anche il numero di moli di ![]() nella
soluzione finale, per cui la molarita' e' ottenuta immediatamente
(notate la trasformazione del volume
nella
soluzione finale, per cui la molarita' e' ottenuta immediatamente
(notate la trasformazione del volume ![]() in
in ![]() ):
):
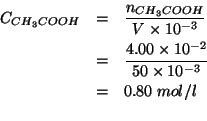
Per la frazione molare, partendo dalla definizione:

Dati:
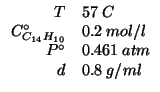
Altri simboli:
|
|
massa molare di |
| massa molare di |
|
| massa in |
|
|
|
massa di |
| massa di |
|
|
|
numero di moli di |
| numero di moli di |
Per comodita', ragioniamo su ![]() di soluzione, la cui massa in
grammi sara':
di soluzione, la cui massa in
grammi sara':
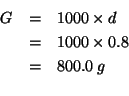
La massa in grammi di ![]() contenuta nella massa di
soluzione considerata e':
contenuta nella massa di
soluzione considerata e':

Ovviamente, il resto e' benzene:
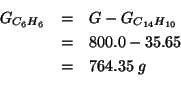
Ora troviamo la frazione molare di ![]() :
:
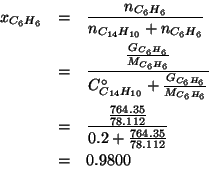
Infine, la tensione di vapore della soluzione:
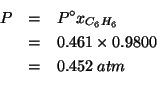
Dati:

Altri simboli:
| massa molare del composto in |
|
| molalita' della soluzione | |
| numero di moli del composto |
Scriviamo la legge dell'innalzamento ebullioscopico in funzione della massa molare del soluto:
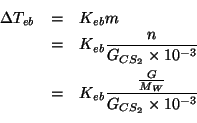
da cui:
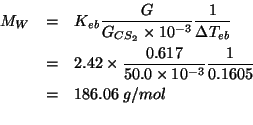
| ioduro di idrogeno |
| ossido di dibromo |
| anidride periodica |
| ossido rameico |
| idrossido di magnesio |
| acido ipoiodoso |
| acido bromico |
| nitrato di magnesio |
| fosfato di alluminio |
| idrogenofosfato di piombo (II) |
| perclorato di argento |
(Questo esercizio vale ![]() punti)
punti)
| ioduro di idrogeno | |
| ossido di dibromo | |
| anidride periodica | |
| ossido rameico | |
| idrossido di magnesio |
|
| acido ipoiodoso | |
| acido bromico | |
| nitrato di magnesio |
|
| fosfato di alluminio | |
| idrogenofosfato di piombo (II) |
|
| perclorato di argento |
(Questo esercizio vale ![]() punti)
punti)
Applicando il metodo visto durante il corso si ottiene:
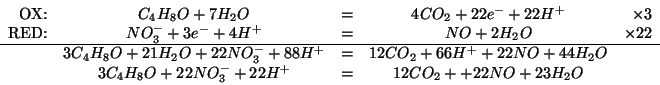
Facendo reagire a una certa temperatura ![]() di
di ![]() con
con
![]() di
di ![]() , quando l'equilibrio e' raggiunto si sono
formate
, quando l'equilibrio e' raggiunto si sono
formate ![]() di
di ![]() e la pressione totale nel recipiente
di reazione e'
e la pressione totale nel recipiente
di reazione e' ![]() . Calcolate la costante
. Calcolate la costante ![]() per la
reazione a quella temperatura. (Questo esercizio vale
per la
reazione a quella temperatura. (Questo esercizio vale ![]() punti)
punti)
Dati:
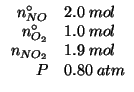
Altri simboli:
| NO | numero di moli di |
| O_2 | numero di moli di |
| frazione molare di |
|
| frazione molare di |
|
| frazione molare di |
Dalla stechiometria della reazione e dai dati del problema e' facile ricavare il numero di moli di ciascun componente all'equilibrio:
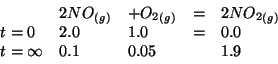
Avendo il numero di moli di ciascun componente all'equilibrio, ricaviamo le corrispondenti frazioni molari:
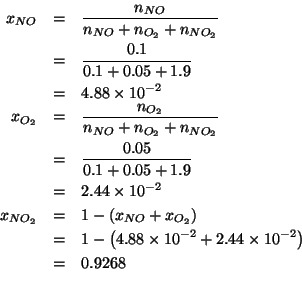
Infine:
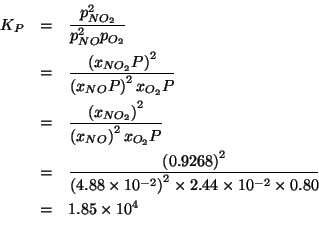
sapendo che:
![]() e
e
![]() . (Questo esercizio vale
. (Questo esercizio vale ![]() punti)
punti)
Dati:
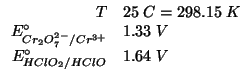
Altri simboli:
| costante di Faraday: |
|
| costante dei gas:
|
|
| numero di elettroni scambiati nella reazione redox |
La relazione che lega la costante di equilibrio della reazione redox alla differenza dei potenziali standard delle due coppie redox coinvolte e':
Il numero di elettroni scambiati nella reazione e' ![]() (basta
considerare una delle due coppie redox e valutare il cambiamento dello
stato di ossidazione).
(basta
considerare una delle due coppie redox e valutare il cambiamento dello
stato di ossidazione).
Quindi:
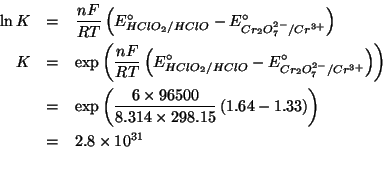
Dati:
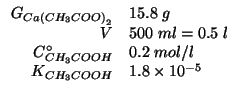
Altri simboli:
|
|
massa molare di
|
|
|
numero di moli di |
|
|
numero di moli di |
|
|
numero di moli di
|
Il sistema ottenuto e' ovviamente una soluzione tampone basata sulla
coppia coniugata
![]() . Si puo' quindi applicare la
formula ricavata durante il corso:
. Si puo' quindi applicare la
formula ricavata durante il corso:
Per trovare il numero di moli della forma acida e basica:
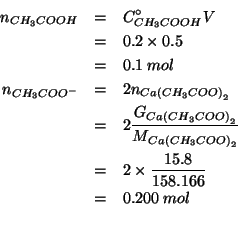
Quindi:
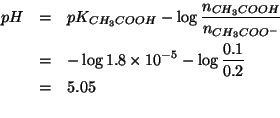
Dati:
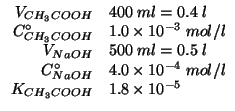
Altri simboli:
| prodotto ionico dell'acqua:
|
|
| costante di ionizzazione basica dello ione acetato | |
|
|
numero di moli di acido acetico |
|
|
numero di moli di ione ossidrile |
La reazione cha avviene all'atto del mescolamento e':
La costante di equilibrio di questa reazione acido base e' molto grande. Infatti, la reazione e' l'inversa della ionizzazione basica dello ione acetato e quindi la sua costante di equilibrio e' data da:
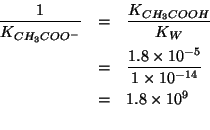
La reazione si puo' quindi assumere completa. Il reagente limitante e' chiaramente lo ione ossidrile, poiche' si mescolano volumi molto simili, ma la concentrazione dello ione ossidrile e' sensibilmente minore di quella dell'acido acetico. Allora:
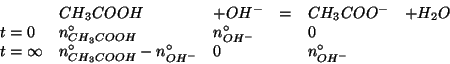
Al termine della reazione, la soluzione contiene acido acetico e ione
acetato in quantita' comparabili: si tratta quindi di una soluzione
tampone. Il ![]() si ottiene allora da:
si ottiene allora da: