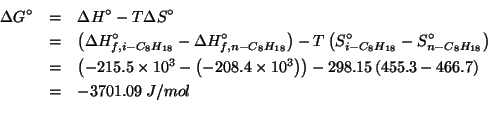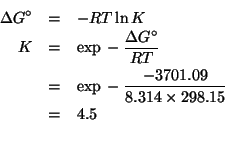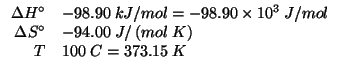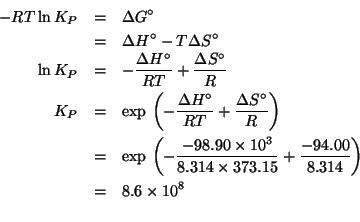Dati:
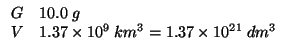
Altri simboli:
| massa molare dell'acqua: |
|
| numero di moli | |
| numero totale di molecole di acqua | |
| numero di molecole di acqua per litro | |
| numero di Avogadro:
|
Il numero di molecole di acqua (inizialmente contenute nel cucchiaio) per litro di acqua di mare dopo il mescolamento e' dato da:
Il numero totale di molecole d'acqua contenute in ![]() grammi
si ottiene immediatamente trasformando prima in moli (tramite la massa
molare) e utilizzando poi il numero di Avogadro:
grammi
si ottiene immediatamente trasformando prima in moli (tramite la massa
molare) e utilizzando poi il numero di Avogadro:
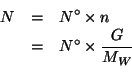
Quindi:
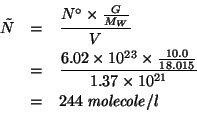
Calcolate il volume di cloro gassoso, misurato a ![]() e
e
![]() , che si sviluppa in seguito all'ossidazione di
, che si sviluppa in seguito all'ossidazione di ![]() di cloruro di mercurio (I).
di cloruro di mercurio (I).
Dati:
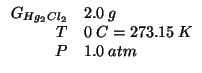
Altri simboli:
|
|
massa molare di |
|
|
numero di moli di |
| numero di moli di |
|
| costante dei gas:
|
Dalla stechiometria della semiequazione si ricava:
Il numero di moli di ![]() si ricava dalla massa in grammi e
dalla massa molare:
si ricava dalla massa in grammi e
dalla massa molare:
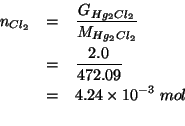
Il volume occupato dal cloro gassoso nelle condizioni date si trova applicando la legge dei gas ideali:
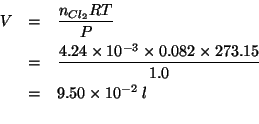
in soluzione acquosa basica. Completate e bilanciate questa equazione.
(Suggerimenti: il ![]() non cambia stato di ossidazione; nella
semireazione di riduzione, l'ossigeno molecolare si riduce a ione ossidrile)
non cambia stato di ossidazione; nella
semireazione di riduzione, l'ossigeno molecolare si riduce a ione ossidrile)
L'elemento che si ossida e' lo zolfo, quello che si riduce e' l'ossigeno.
Applicando il metodo visto durante il corso:
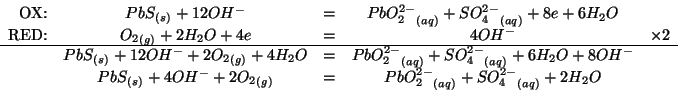
Dati:
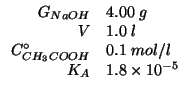
Altri simboli:
| massa molare di |
|
|
|
numero di moli iniziale di |
|
|
concentrazione iniziale di |
| prodotto ionico dell'acqua:
|
|
| costante di ionizzazione basica dello ione acetato |
L'idrossido di sodio e' una base forte, quindi in soluzione si
dissocia in ioni ![]() e ioni
e ioni ![]() . L'acido acetico, invece,
e' un tipico acido debole, dissociato solo in minima parte. La
reazione da considerare e' quindi:
. L'acido acetico, invece,
e' un tipico acido debole, dissociato solo in minima parte. La
reazione da considerare e' quindi:
La costante di equilibrio ![]() di questa reazione si trova facilmente
osservando che essa e' l'inversa della ionizzazione basica dello ione
acetato e quindi:
di questa reazione si trova facilmente
osservando che essa e' l'inversa della ionizzazione basica dello ione
acetato e quindi:

La reazione si puo' quindi considerare completa. Per vedere qual'e' il
reagente limitante, valutiamo la concentrazione iniziale di ioni
![]() , ovviamente uguale alla concentrazione iniziale di
, ovviamente uguale alla concentrazione iniziale di ![]() .
.
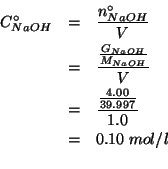
Si vede quindi che ![]() e acido acetico sono in rapporto
stechiometrico. Allora, assumendo la reazione completa:
e acido acetico sono in rapporto
stechiometrico. Allora, assumendo la reazione completa:
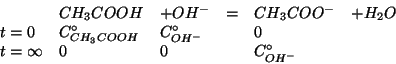
Come visto durante il corso, un miglior valore per la concentrazione
finale di ioni ![]() (che ovviamente non puo' essere nulla) puo'
essere ottenuto sfruttando la legge dell'azione di massa e il fatto
che, date le condizioni iniziali, all'equilibrio deve essere:
(che ovviamente non puo' essere nulla) puo'
essere ottenuto sfruttando la legge dell'azione di massa e il fatto
che, date le condizioni iniziali, all'equilibrio deve essere:
Quindi:
Si sa che il composto e' un elettrolita forte che si dissocia secondo l'equazione:
La pressione osmotica della soluzione a ![]() e' pari a
e' pari a
![]() .
.
Determinate la massa molare del composto.
Dati:
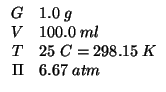
Altri simboli:
| costante dei gas:
|
|
| concentrazione molare colligativa | |
| numero di moli colligativo | |
| numero di moli del composto incognito | |
| massa molare |
Applichiamo la legge della pressione osmotica:
La concentrazione colligativa puo' essere espressa in base alla definizione di concentrazione molare:
Siccome il composto si dissocia completamente in ![]() ioni, il numero
di moli colligativo e' pari a
ioni, il numero
di moli colligativo e' pari a ![]() volte il numero di moli del
composto:
volte il numero di moli del
composto:
Infine, il numero di moli del composto puo' essere espresso in funzione dalla massa molare cercata:
Risolvendo rispetto a ![]() :
:
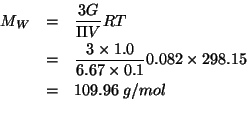

Determinate la formula molecolare del composto.
Dati:
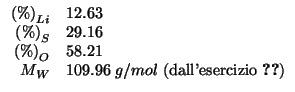
Altri simboli:
| Li | numero di moli di litio |
| S | numero di moli di zolfo |
| O | numero di moli di ossigeno |
| Li | massa di litio |
| S | massa di zolfo |
| O | massa di ossigeno |
| Li | massa molare del litio: |
| S | massa molare dello zolfo: |
| O | massa molare dell' ossigeno: |
Prendiamo come riferimento una massa molare del composto (il cui
valore abbiamo determinato risolvendo
l'esercizio ![]() ).
).
Allora:
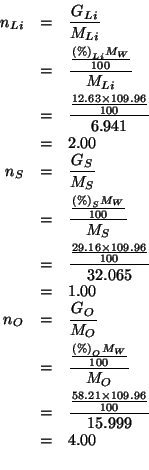
Si trattava quindi del solfato di litio: ![]()
Applichiamo il metodo per la costruzione delle formule di Lewis illustrato durante il corso:
| Elettroni di valenza | |
| carica | -2 |
| totale | |
Ponendo l'atomo di zolfo (meno elettronegativo) al centro si ottiene come prima possibilita':
![\begin{displaymath}
(a):\;\left[
\begin{xy}
<1em,0em>:
*+{S},c=''S'';
p+/l2em/*...
...\vert},
p+/r0.1em/**\dir{}?<*\dir{\vert},
\end{xy}\right]^{2-}
\end{displaymath}](img87.gif)
Tuttavia, essendo del terzo periodo, lo zolfo puo' presentare valenza espansa. Si hanno cosi' le seguenti ulteriori possibilita' (per ognuna di esse, non riportiamo le eventuali formule identiche contenenti lo stesso numero di legami doppi):
![\begin{displaymath}
\begin{array}{ccc}
(b):\;\left[
\begin{xy}
<1em,0em>:
*+{S}...
...m/**\dir{}?<*\dir{\vert},
\end{xy}\right]^{2-}
&\\
\end{array}\end{displaymath}](img88.gif)
Per poter decidere quale delle strutture e' la piu' stabile, ricorriamo al criterio della carica atomica formale. Applicando la definizione e il metodo per la sua determinazione si ottiene:
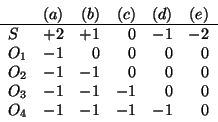
Da quest'analisi si vede chiaramente che la struttura piu' stabile
sara' la
![]() , perche' ha le cariche minori possibile
disposte nel modo piu' ragionevole (cariche negative sugli atomi di
ossigeno e non sull'atomo di zolfo).
, perche' ha le cariche minori possibile
disposte nel modo piu' ragionevole (cariche negative sugli atomi di
ossigeno e non sull'atomo di zolfo).
Per la geometria molecolare, applichiamo il modello VSEPR, basandoci
su una qualsiasi delle strutture di Lewis disegnate, ad esempio la
![]() .
.
| coppie strutturali | 4 | |
| geometria delle coppie strutturali |
|
|
| coppie di non legame | 0 | |
| geometria molecolare | tetraedrica |
Infine, essendo la geometria delle coppie strutturali tetraedrica,
l'ibridazione dell'atomo di zolfo sara' di tipo ![]() .
.

Dati:

Lo stronzio appartiene al secondo gruppo e al quinto periodo della
tavola periodica; il suo numero atomico e' ![]() . Applicando il
semplice schema visto durante il corso si ha:
. Applicando il
semplice schema visto durante il corso si ha:

e quindi la configurazione elettronica dello stato fondamentale e':
Dalla configurazione elettronica si vede che lo strato di valenza
dello stronzio e': ![]() .
.
Allora l'andamento delle energie di ionizzazione puo' essere
commentato come segue. L'energia di ionizzazione cresce nell'ordine
![]() perche' e' sempre piu' difficile strappare un
elettrone man mano che il sistema atomico acquista una carica positiva
sempre maggiore:
perche' e' sempre piu' difficile strappare un
elettrone man mano che il sistema atomico acquista una carica positiva
sempre maggiore:
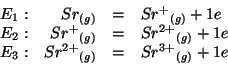
Inoltre, si puo' vedere che
![]() . Cio' e' dovuto al
fatto che il terzo elettrone estratto e' un elettrone
. Cio' e' dovuto al
fatto che il terzo elettrone estratto e' un elettrone ![]() :
appartiene, cioe', a uno strato interno, ed e' quindi molto piu'
costosa la sua estrazione.
:
appartiene, cioe', a uno strato interno, ed e' quindi molto piu'
costosa la sua estrazione.
I potenziali standard delle due coppie redox sono:
![]() e
e
![]() .
.
Dati:
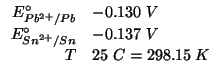
Altri simboli:
| costante di Faraday: |
|
| costante dei gas:
|
In pratica si deve valutare la spontaneita' o meno della reazione rappresentata dall'equazione data. Siccome il sistema non si trova in condizioni standard, bisogna valutare i potenziali di riduzione nelle condizioni non standard usando l'equazione di Nernst:
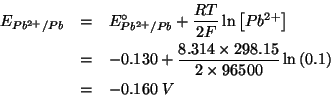
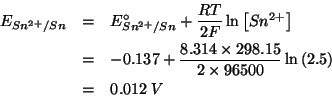
Si vede che
![]() e quindi se ne conclude
che la reazione non e' spontanea: la sbarretta di stagno non verra'
attaccata dagli ioni
e quindi se ne conclude
che la reazione non e' spontanea: la sbarretta di stagno non verra'
attaccata dagli ioni ![]() .
.
Dati:
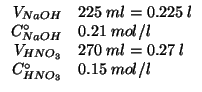
Altri simboli:
| prodotto ionico dell'acqua:
|
|
|
|
numero di moli iniziale di |
| numero di moli iniziale di |
|
| numero di moli finale di |
Sia la base che l'acido sono forti e quindi completamente dissociati. La reazione che avviene all'atto del mescolamento e' pertanto:
Tale reazione e' l'inversa dell'autoionizzazione dell'acqua e quindi
la sua costante di equilibrio e':
![]() .
.
Siccome la costante di equilibrio e' molto grande, la reazione puo' essere considerata (in prima approssimazione) completa.
Si deve allora valutare il reagente limitante:
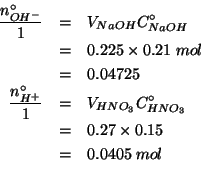
Il reagente limitante e' quindi l'acido nitrico (cioe' gli ioni
![]() sono in difetto rispetto agli ioni
sono in difetto rispetto agli ioni ![]() ). Gli ioni
). Gli ioni ![]() verranno completamente consumati, mentre la quantita' finale di ioni
verranno completamente consumati, mentre la quantita' finale di ioni
![]() sara':
sara':
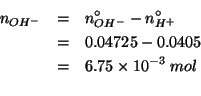
Per avere la concentrazione basta dividere per il volume totale:
![\begin{eqnarray*}
\left[OH^-\right]&=&\frac{\NOf{OH^-}}{\VOf{NaOH}+\VOf{HNO_3}}\...
...10^{-2}\;mol/l\\ %(/ 6.75e-3 (+ 0.225 0.27))0.013636363636363636
\end{eqnarray*}](img131.gif)
Infine, per il ![]() :
:
![\begin{eqnarray*}
pH&=&14.0-pOH\\
&=&14.0-\left(-\log\left[OH^-\right]\right)\\...
...ht)\\
&=&12.13\\ %(- 14.0 (-(log10 1.36e-2)))12.133538908370218
\end{eqnarray*}](img132.gif)