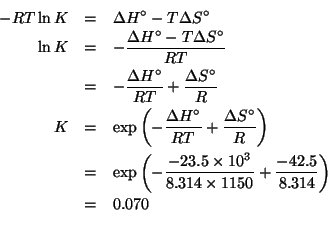Il fosforo appartiene al quindicesimo gruppo e al terzo periodo della
tavola periodica; il suo numero atomico e' ![]() . Applicando il
semplice schema visto durante il corso si ha:
. Applicando il
semplice schema visto durante il corso si ha:

e quindi la configurazione elettronica dello stato fondamentale e':
I ![]() elettroni
elettroni ![]() sono sistemati uno per ciascuno dei
sono sistemati uno per ciascuno dei ![]() orbitali degeneri
orbitali degeneri ![]() , con spin parallelo in base alla regola di
Hund. Cio' viene messo in evidenza con la notazione a caselle:
, con spin parallelo in base alla regola di
Hund. Cio' viene messo in evidenza con la notazione a caselle:
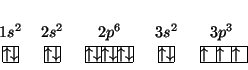
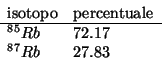
Calcolate (riportando il risultato in Da con ![]() cifre decimali) la
sua massa atomica geonormale. Per il calcolo assumete che le masse
delle particelle subatomiche (protone, neutrone ed elettrone) siano:
cifre decimali) la
sua massa atomica geonormale. Per il calcolo assumete che le masse
delle particelle subatomiche (protone, neutrone ed elettrone) siano:
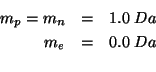
Dati:
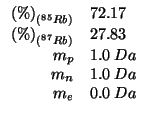
Altri simboli:
|
|
massa atomica dell'isotopo |
|
|
massa atomica dell'isotopo |
Con i valori approssimati delle masse delle particelle subatomiche dati, le masse atomiche dei due isotopi coincidono coi rispettivi numeri di massa:
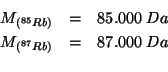
Allora la massa atomica geonormale e' data da:
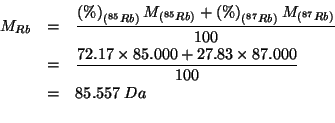
Il valore corretto della massa atomica del rubidio e' ![]() .
.
Dati:
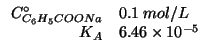
Altri simboli:
| prodotto ionico dell'acqua:
|
Il benzoato di sodio e' un sale e come tale e' completamente dissociato in soluzione acquosa. Lo ione sodio ha proprieta' acide trascurabili, essendo l'acido coniugato di una base forte (l'idrossido di sodio). Lo ione benzoato ha invece proprieta' basiche apprezzabili, in quanto base coniugata di un acido debole (l'acido benzoico).
Quindi, in seguito all'introduzione del sale in acqua, si avra' la reazione:
E' chiaro che il ![]() della soluzione sara' basico, cioe' maggiore
di
della soluzione sara' basico, cioe' maggiore
di ![]() . Il calcolo e' ovviamente quello per trovare il
. Il calcolo e' ovviamente quello per trovare il ![]() di una
soluzione contenente una base debole; la formula finale, ricavata
durante il corso, e':
di una
soluzione contenente una base debole; la formula finale, ricavata
durante il corso, e':
![]() e' la costante di ionizzazione basica dello ione
benzoato. Essa puo' essere ricavata immediatamente conoscendo la
costante di ionizzazione acida dell'acido benzoico e quella del prodotto
ionico dell'acqua. Infatti deve valere:
e' la costante di ionizzazione basica dello ione
benzoato. Essa puo' essere ricavata immediatamente conoscendo la
costante di ionizzazione acida dell'acido benzoico e quella del prodotto
ionico dell'acqua. Infatti deve valere:
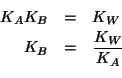
![]() e' la concentrazione iniziale dello ione benzoato. Per
ovvie ragioni di stechiometria si ha:
e' la concentrazione iniziale dello ione benzoato. Per
ovvie ragioni di stechiometria si ha:
Infine:
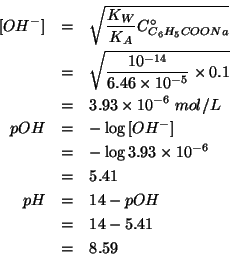
Dati:
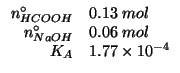
Altri simboli:
| prodotto ionico dell'acqua:
|
E' un caso di preparazione di un tampone mediante una reazione acido
base che trasforma una parte dell'acido debole nella corrispondente
base coniugata: gli ioni ![]() provenienti dall'idrossido di sodio
reagiscono con una parte dell'acido formico (dai numeri di moli si
vede immediatamente che gli ioni ossidrile sono in difetto
stechiometrico); la reazione e' praticamente completa perche' e'
l'inversa della ionizzazione basica dello ione formiato. La costante
provenienti dall'idrossido di sodio
reagiscono con una parte dell'acido formico (dai numeri di moli si
vede immediatamente che gli ioni ossidrile sono in difetto
stechiometrico); la reazione e' praticamente completa perche' e'
l'inversa della ionizzazione basica dello ione formiato. La costante ![]() di ionizzazione basica di quest'ultimo e' legata alla costante di
ionizzazione acida dell'acido formico dalla relazione:
di ionizzazione basica di quest'ultimo e' legata alla costante di
ionizzazione acida dell'acido formico dalla relazione:
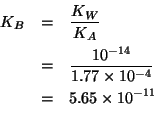
Quindi, la reazione fra acido formico e ioni ossidrile ha una costante
di equilibrio pari a
![]() .
.
Assumendo la reazione completa si ha:
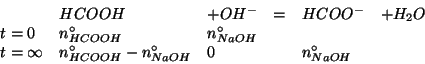
Dopo questa reazione, la soluzione contiene
![]() moli di acido formico e
moli di acido formico e
![]() moli di formiato. Si puo' immediatamente ottenere
il
moli di formiato. Si puo' immediatamente ottenere
il ![]() applicando la formula ricavata durante il corso:
applicando la formula ricavata durante il corso:
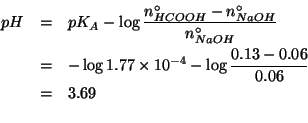
Dati:
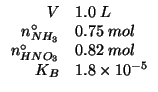
Altri simboli:
| prodotto ionico dell'acqua:
|
L'ammoniaca e' una base debole. L'acido nitrico e' un acido forte, quindi completamente ionizzato in soluzione acquosa. La reazione che avverra' all'atto del mescolamento e' quindi:
La costante di equilibrio di questa reazione acido base si trova
subito osservando che essa e' l'inversa della ionizzazione acida dello
ione ammonio. La costante di ionizzazione acida ![]() dello ione
ammonio e' legata alla costante di ionizzazione basica dell'ammoniaca
dalla relazione:
dello ione
ammonio e' legata alla costante di ionizzazione basica dell'ammoniaca
dalla relazione:
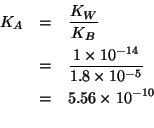
La reazione su scritta ha dunque una costante di equilibrio pari a
![]() e quindi si puo' considerare completa.
e quindi si puo' considerare completa.
E' immediato rendersi conto che il reagente limitante e' l'ammoniaca, per cui:
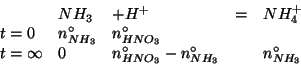
La concentrazione finale di ioni ![]() e' ricavata subito dal
corrispondente numero di moli:
e' ricavata subito dal
corrispondente numero di moli:

e quindi il ![]() e':
e':
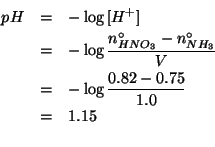
![\begin{psfrags}\psfrag{P} [r][r]{{$P\;(atm)$}}\psfrag{PC} [r][r]{{$47.2$}}...
...rag{TC} [c][c]{{$823.0$}}
\includegraphics{state-diag-generic.eps}
\end{psfrags}](img62.gif)
In quale intervallo di pressione e' possibile sublimare il solido mediante riscaldamento a pressione costante?
Dati:

Come visto durante il corso, la sublimazione e' il passaggio dalla fase solida alla fase gassosa. Affinche' questa transizione di stato possa avvenire per riscaldamento a pressione costante (per la sostanza in questione), deve essere possibile passare con un cammino rettilineo orizzontale dalla zona di equilibrio del solido a quella del gas senza attraversare la zona di equilibrio del liquido. Dal diagramma di stato e' facile rendersi conto che cio' e' possibile solo per pressioni inferiori alla pressione del punto triplo. L'intervallo di pressione richiesto e' quindi:
![\begin{psfrags}\psfrag{P} [r][r]{{$P\;(atm)$}}\psfrag{PC} [r][r]{{$47.2$}}...
... [c][c]{{$823.0$}}
\includegraphics{state-diag-generic-solved.eps}
\end{psfrags}](img65.gif)
Dati:
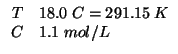
Altri simboli:
| costante dei gas:
|
Essendo il composto un non elettrolita, ricorrendo all'espressione che lega la pressione osmotica alla concentrazione molare si ottiene immediatamente:

Dati:
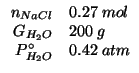
Altri simboli:
| frazione molare del solvente | |
| numero di moli di ioni |
|
| numero di moli di ioni |
|
| numero di moli di |
|
| massa molare dell'acqua: |
L'espressione che fornisce la pressione di vapore di una soluzione
(ideale) in funzione della concentrazione del solvente e':
La frazione molare del solvente deve tenere conto dell'eventuale comportamento elettrolitico del soluto. Nel caso in esame il soluto introdotto in soluzione e' un sale e quindi un elettrolita forte che si dissocia secondo:
Di conseguenza, la frazione molare e' calcolata come:
Ovviamente:
Inoltre:
Quindi:
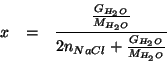
e infine:
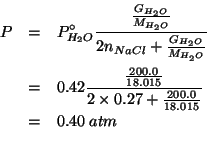
Dati:
![]()
Altri simboli:
| numero di moli di |
|
| massa molare di |
|
| numero di moli di |
|
| massa molare di |
Per prima cosa scriviamo l'equazione di combustione bilanciata:
Siccome la combustione e' completa, tutto il butano verra' consumato. Allora:
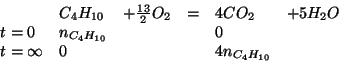
(nella tabella abbiamo evidenziato solo cio' che ci interessa)
Le moli di butano inizialmente poste a reagire sono date da:
Infine:
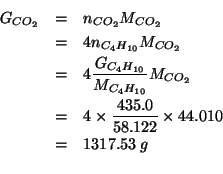
Applicando il metodo visto durante il corso: