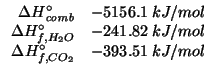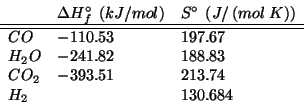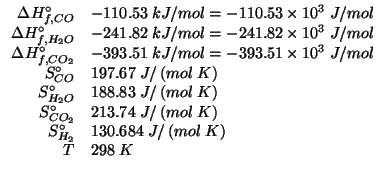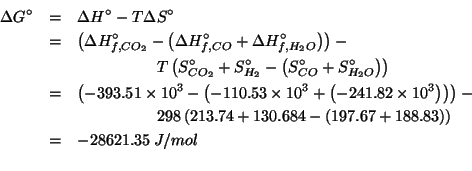e' completa. Si pongono a reagire ![]() di
di ![]() ,
,
![]() di
di ![]() e
e ![]() di
di ![]() .
.
Determinate la massa in grammi di reagenti e prodotti alla fine della reazione.
Dati:
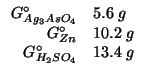
Altri simboli:
|
|
numero di moli iniziale di |
| numero di moli iniziale di |
|
|
|
numero di moli iniziale di |
| numero di moli di |
|
| numero di moli di |
|
| numero di moli di |
|
| numero di moli di |
|
| numero di moli di |
|
| numero di moli di |
|
| numero di moli di |
|
| numero di moli di |
|
|
|
massa molare di |
| massa molare di |
|
|
|
massa molare di |
| massa molare di |
|
| massa molare di |
|
| massa molare di |
|
| massa molare di |
|
| massa di |
|
| massa di |
|
| massa di |
|
| massa di |
|
| massa di |
|
| massa di |
Per prima cosa trasformiamo le quantita' date in grammi nei corrispondenti numeri di moli.
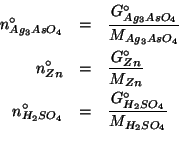
Ora dobbiamo determinare il reagente limitante: a tale scopo valutiamo il rapporto fra il numero di moli iniziale e il rispettivo coefficiente stechiometrico per ciascun reagente.
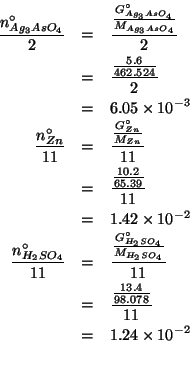
E' evidente che il reagente limitante e' ![]() : al termine
della reazione, quindi, esso sara' completamente consumato.
: al termine
della reazione, quindi, esso sara' completamente consumato.
Inoltre, potremo basarci su di esso per ricavare il numero di moli di tutti gli altri partecipanti al termine della reazione.
Ad esempio, sapendo quante moli di ![]() hanno reagito e
conoscendo il rapporto stechiometrico fra
hanno reagito e
conoscendo il rapporto stechiometrico fra ![]() e
e ![]() , e'
immediato ricavare il numero di moli di
, e'
immediato ricavare il numero di moli di ![]() che hanno reagito:
che hanno reagito:
e quindi il numero di moli di ![]() che rimarranno a fine reazione
e':
che rimarranno a fine reazione
e':
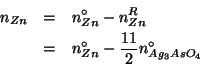
In modo identico:
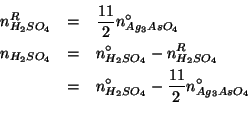
Sempre basandoci sul numero di moli iniziale di ![]() , possiamo
ricavare facilmente il numero di moli di ciascun prodotto:
, possiamo
ricavare facilmente il numero di moli di ciascun prodotto:
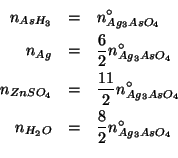
Infine, non resta che trasformare i numeri di moli cosi' ottenuti nelle corrispondenti masse in grammi:
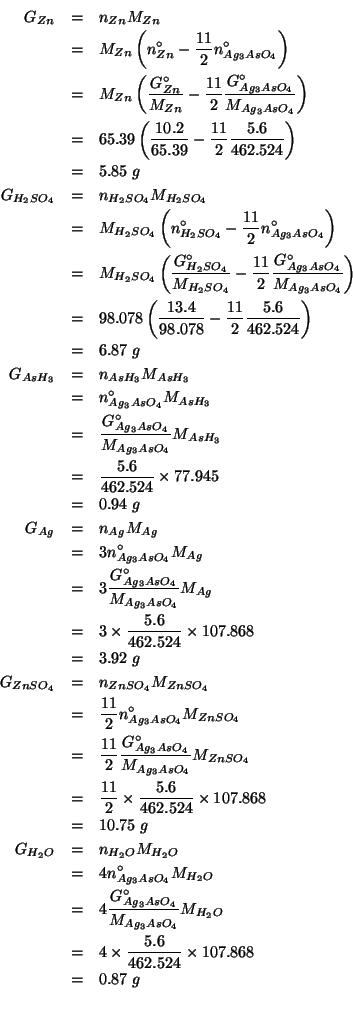
Dati:
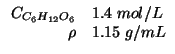
Altri simboli:
|
|
numero di moli di glucosio |
| massa della soluzione in grammi | |
|
|
massa di glucosio in grammi |
|
|
massa molare del glucosio:
|
Consideriamo un litro di soluzione (cioe' ![]() ). E' chiaro che
la sua massa sara':
). E' chiaro che
la sua massa sara':
In tale massa di soluzione sono contenute, per definizione di
concentrazione molare,
![]() di glucosio,
corrispondenti a:
di glucosio,
corrispondenti a:
grammi di glucosio.
Non resta che calcolare la percentuale in massa richiesta:
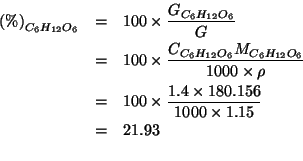
Dopo che il sistema ha raggiunto l'equilibrio si trova che la
pressione totale e' ![]() e nel recipiente sono presenti
e nel recipiente sono presenti
![]() di
di ![]() ,
, ![]() di
di ![]() e
e ![]() di
di
![]() . Determinate la costante di equilibrio
. Determinate la costante di equilibrio ![]() della reazione
(alla temperatura dell'esperimento) espressa in funzione delle
pressioni parziali.
della reazione
(alla temperatura dell'esperimento) espressa in funzione delle
pressioni parziali.
Dati:
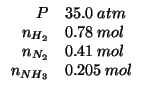
Altri simboli:
| numero totale di moli presenti all'equilibrio | |
| frazione molare di |
|
| frazione molare di |
|
| frazione molare di |
|
| pressione parziale di |
|
| pressione parziale di |
|
| pressione parziale di |
Per prima cosa calcoliamo le frazioni molari all'equilibrio:
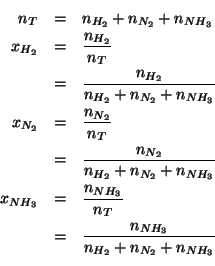
Ora ci possiamo calcolare le pressioni parziali:
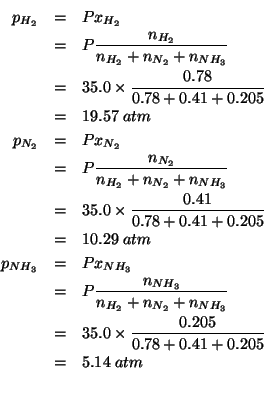
Non resta che calcolare la ![]() :
:
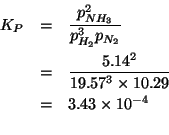
- la formula di Lewis piu' stabile
- la geometria molecolare
Applichiamo il metodo per scrivere le formule di Lewis visto durante il corso.
| Elettroni di valenza | |
| carica | |
| totale | |
Ponendo l'atomo di ![]() (meno elettronegativo) al centro, si
ottiene:
(meno elettronegativo) al centro, si
ottiene:
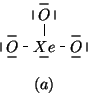
Questa e' solo la prima formula accettabile, in cui l'atomo centrale
(oltre, ovviamente, agli atomi terminali)
e' circondato da otto elettroni. Tuttavia, siccome lo xenon
appartiene al quinto periodo, puo' dare valenza espansa. Quindi, oltre
alla ![]() , si possono scrivere le seguenti formule di Lewis:
, si possono scrivere le seguenti formule di Lewis:
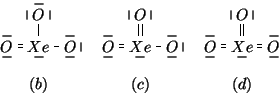
Chiaramente, la formula ![]() esiste in
esiste in ![]() versioni identiche
tranne che per la posizione del doppio legame. Lo stesso vale per la
formula
versioni identiche
tranne che per la posizione del doppio legame. Lo stesso vale per la
formula ![]() , in cui le tre versioni identiche differiscono solo
per la posizione del legame singolo.
, in cui le tre versioni identiche differiscono solo
per la posizione del legame singolo.
Per decidere quale formula di Lewis sia piu' stabile bisogna valutare le cariche atomiche formali. Applicando il metodo visto a lezione si ha:
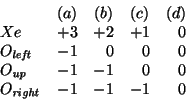
Si vede quindi che la formula piu' stabile e' la ![]() , in cui tutte
le cariche atomiche formali sono nulle.
, in cui tutte
le cariche atomiche formali sono nulle.
Per determinare la geometria molecolare applichiamo il metodo
VSEPR. Consideriamo una qualsiasi delle formule di Lewis scritte: ci
sono ![]() coppie strutturali e quindi la geometria delle coppie
strutturali sara' tetraedrica. Siccome c'e' una coppia di non legame,
la geometria molecolare sara' piramidale trigonale.
coppie strutturali e quindi la geometria delle coppie
strutturali sara' tetraedrica. Siccome c'e' una coppia di non legame,
la geometria molecolare sara' piramidale trigonale.
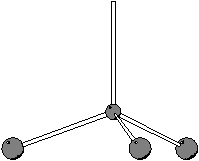 |
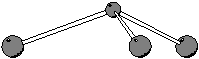 |
| geometria delle coppie strutturali | geometria molecolare |
Per prima cosa scriviamo tutte le possibili formule di Lewis dello ione molecolare. Applicando il metodo visto durante il corso si ha:
| Elettroni di valenza | |
| carica | |
| totale | |
Ponendo l'atomo di ![]() (meno elettronegativo) al centro, si
ottiene:
(meno elettronegativo) al centro, si
ottiene:
![\begin{displaymath}
\begin{array}{c}
\left[\begin{xy}
<1em,0em>:
*+{N},c=''N'';...
...*\dir{}?<*\dir{\vert},
\end{xy}\right]^-
\\ \\
(a)
\end{array}\end{displaymath}](img112.gif)
La formula ottenuta non e' accettabile perche' l'atomo di azoto non e'
circondato da ![]() elettroni. Utilizzando una coppia solitaria di un
atomo di ossigeno per formare un legame
elettroni. Utilizzando una coppia solitaria di un
atomo di ossigeno per formare un legame ![]() con l'azoto si hanno
tre possibilita' equivalenti:
con l'azoto si hanno
tre possibilita' equivalenti:
![\begin{displaymath}
\begin{array}{ccc}
\left[\begin{xy}
<1em,0em>:
*+{N},c=''N'...
...{\vert},
\end{xy}\right]^-
\\
&&\\
(b)&(c)&(d)\\
\end{array}\end{displaymath}](img114.gif)
Non ci sono altre possibilita', dal momento che l'azoto, appartenendo al secondo periodo, non puo' dare valenza espansa.
E' chiaro che le tre formule di risonanza possibili sono fra loro
equivalenti, differendo unicamente per la posizione del doppio legame:
ne segue che ciascuna contribuisce in modo identico all'ibrido e
quindi i tre legami ![]() sono perfettamente identici.
sono perfettamente identici.
Consideriamo allora uno qualsiasi di essi, ad esempio quello fra l'azoto e l'ossigeno di sinistra: il suo ordine sara' la media sulle tre formule di risonanza:
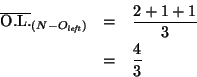
Dati:
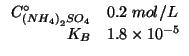
Altri simboli:
| costante di ionizzazione acida dello ione ammonio | |
| prodotto ionico dell'acqua:
|
![]() e' un sale e quindi in acqua e'
completamente dissociato in ioni
e' un sale e quindi in acqua e'
completamente dissociato in ioni ![]() e ioni
e ioni ![]() ,
secondo:
,
secondo:
Lo ione solfato e' la base coniugata di un acido forte e quindi la sua forza basica e' effettivamente nulla.
Lo ione ![]() e' l'acido coniugato dell'ammoniaca, che, come
mostra il valore della sua costante basica, e' una base debole. Ne
segue che lo ione ammonio ha una forza acida non trascurabile: essa e'
misurata da una
e' l'acido coniugato dell'ammoniaca, che, come
mostra il valore della sua costante basica, e' una base debole. Ne
segue che lo ione ammonio ha una forza acida non trascurabile: essa e'
misurata da una ![]() che si ricava da:
che si ricava da:
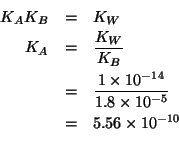
Il problema e' quindi quello di trovare il ![]() di una soluzione
contenente un acido debole (lo ione ammonio):
di una soluzione
contenente un acido debole (lo ione ammonio):
La formula finale e' stata ricavata durante il corso:
Chiaramente, guardando l'equazione che descrive la dissociazione del sale, deve valere:
Quindi:
![\begin{eqnarray*}
\left[H^+\right]&=&\sqrt{2\CZeroOf{\left(NH_4\right)_2SO_4}K_A...
...4.83\\ % (- (log10 (sqrt (* 2.0 0.2 5.56e-10))))4.82643260854499
\end{eqnarray*}](img132.gif)
Il ![]() ottenuto e' acido, come ci si poteva aspettare.
ottenuto e' acido, come ci si poteva aspettare.
Dati:
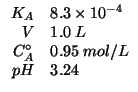
Altri simboli:
| numero di moli di acido lattico | |
| numero di moli di lattato | |
|
|
massa molare del lattato sodico:
|
La formula che da' il ![]() di una soluzione tampone (ricavata
durante il corso) e':
di una soluzione tampone (ricavata
durante il corso) e':
dove ![]() ed
ed ![]() sono, rispettivamente, il numero di moli della
forma acida e quello della forma basica della coppia coniugata su cui
e' basato il tampone.
sono, rispettivamente, il numero di moli della
forma acida e quello della forma basica della coppia coniugata su cui
e' basato il tampone.
Essendo il volume della soluzione pari a ![]() , si ha:
, si ha:
Allora la formula puo' essere utilizzata per trovare il numero di moli di base coniugata (che, ovviamente, e' uguale al numero di moli di sale da aggiungere):
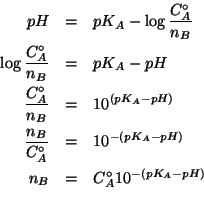
La massa di sale in grammi cercata e' infine:
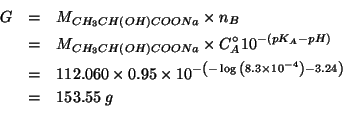
Dati:
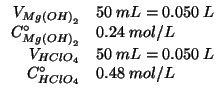
Altri simboli:
| concentrazione di ioni ossidrile e ioni idronio dopo il mescolamento | |
| prodotto ionico dell'acqua:
|
![]() e' una base forte e
e' una base forte e ![]() e' un acido
forte. Entrambi i composti sono quindi completamente ionizzati e la
reazione che avviene all'atto del mescolamento delle due soluzioni e':
e' un acido
forte. Entrambi i composti sono quindi completamente ionizzati e la
reazione che avviene all'atto del mescolamento delle due soluzioni e':
Questa reazione e' l'inversa dell'autoionizzazione dell'acqua e la sua
costante di equilibrio e' quindi ![]() . Essendo la
costante molto grande, la reazione si puo' considerare, in prima
approssimazione, completa. Dobbiamo quindi determinare in primo luogo
il reagente limitante. Questo e' presto fatto se osserviamo che si
mescolano volumi uguali delle due soluzioni e che la concentrazione di
idrossido di magnesio e' la meta' di quella di acido perclorico:
siccome una mole di idrossido di magnesio contiene due moli di ioni
ossidrile, la concentrazione di questi ultimi e quella di ioni idronio
dopo il mescolamento risulteranno uguali.
. Essendo la
costante molto grande, la reazione si puo' considerare, in prima
approssimazione, completa. Dobbiamo quindi determinare in primo luogo
il reagente limitante. Questo e' presto fatto se osserviamo che si
mescolano volumi uguali delle due soluzioni e che la concentrazione di
idrossido di magnesio e' la meta' di quella di acido perclorico:
siccome una mole di idrossido di magnesio contiene due moli di ioni
ossidrile, la concentrazione di questi ultimi e quella di ioni idronio
dopo il mescolamento risulteranno uguali.
In questo caso l'assunzione che la reazione sia completa non e' di grande aiuto, poiche' porterebbe a calcolare un valore nullo sia per la concentrazione di equilibrio degli ioni ossidrile che di quelli idronio:
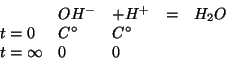
Dobbiamo allora ricorrere alla legge dell'azione di massa, osservando
che, essendo le due concentrazioni iniziali identiche, tali saranno
anche le concentrazioni di equilibrio. Detto ![]() il valore comune di
queste ultime, si ha:
il valore comune di
queste ultime, si ha:
![\begin{eqnarray*}
\frac{1}{K_W}&=&\frac{1}{\left[OH^-\right]\left(H^+\right)}\\
&=&\frac{1}{x^2}
\end{eqnarray*}](img159.gif)
da cui, ovviamente:
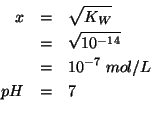
Cioe', come si poteva facilmente prevedere dal momento che gli ioni
ossidrile e gli ioni idronio erano in rapporto stechiometrico: il
![]() della soluzione finale e' uguale a quello dell'acqua pura.
della soluzione finale e' uguale a quello dell'acqua pura.
![]() ,
,
![]() .
.
Dati:
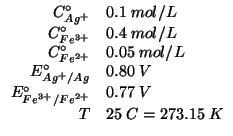
Altri simboli:
| costante dei gas:
|
|
| costante di Faraday: |
In pratica, bisogna stabilire se la reazione:
e' spontanea o meno.
Cio' si puo' fare valutando i potenziali di riduzione delle due coppie redox implicate nelle condizioni date.
Utilizziamo a questo scopo l'equazione di Nernst:
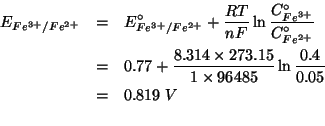
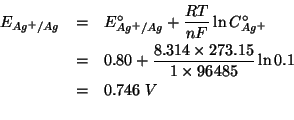
Siccome
![]() , la sbarretta di argento
verra' attaccata dagli ioni ferrici.
, la sbarretta di argento
verra' attaccata dagli ioni ferrici.
Dati:
![]()
Altri simboli:
|
|
massa molare del toluene: |
|
|
numero di moli di toluene |
| numero di moli di carbonio | |
| numero di atomi di carbonio | |
| numero di Avogadro:
|
Il numero di moli di toluene contenuto nella massa in grammi data e':
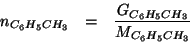
Ogni mole di toluene contiene ![]() di carbonio; quindi il numero
di moli di carbonio e' dato da:
di carbonio; quindi il numero
di moli di carbonio e' dato da:
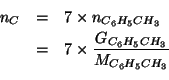
Infine:
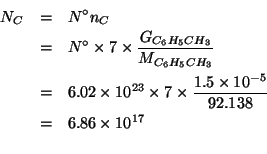
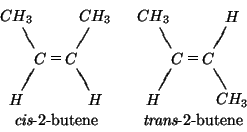
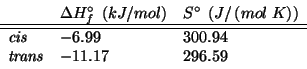
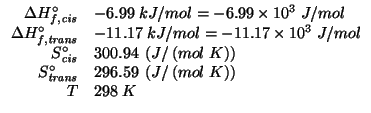
![\begin{eqnarray*}
RT\ln{}K&=&-\Delta{}G^\circ\\
&=&-\left(\Delta{}H^\circ-T\Del...
...296.59-300.94\right)\right)}{8.314\times298}\right]\\
&=&3.2\\
\end{eqnarray*}](img205.gif)