Dati:
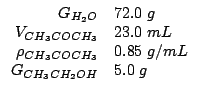
Altri simboli:
| massa molare dell'acqua: |
|
|
|
massa molare dell'acetone: |
|
|
massa dell'acetone in |
|
|
massa molare dell'etanolo: |
| numero di moli dell'acqua | |
|
|
numero di moli dell'acetone |
|
|
numero di moli dell'etanolo |
Per definizione di frazione molare:
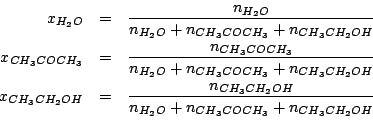
Il numero di moli di ciascun componente e' ottenuto immediatamente dalla massa e dalla massa molare. Nel caso dell'acetone, la massa in grammi e' data dal prodotto fra il volume dato e la densita'. Quindi:
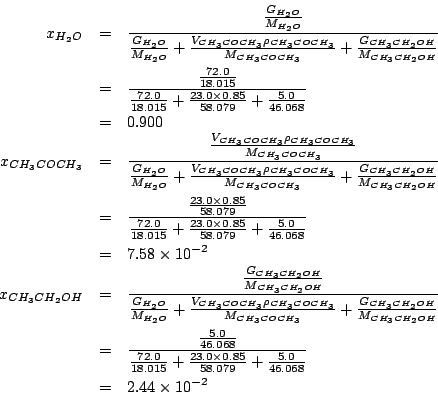
Ovviamente, bastava calcolare due sole frazioni molari e ricavare la terza come complemento ad uno della somma delle prime due.
Dati:
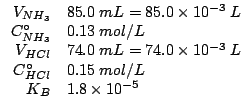
Altri simboli:
|
|
numero di moli iniziale di ammoniaca |
| numero di moli iniziale di acido cloridrico | |
| numero di moli di ioni idronio all'equilibrio | |
| volume totale della soluzione in |
|
| costante di ionizzazione acida dello ione ammonio | |
| prodotto ionico dell'acqua:
|
L'acido cloridrico, essendo un acido forte, e' completamente dissociato; l'ammoniaca, invece, come base debole, e' praticamente tutta indissociata. Quindi, all'atto del mescolamento delle due soluzioni, la reazione che avviene e':
La costante ![]() di questa reazione e' molto grande, perche' la
reazione e' l'inversa della ionizzazione acida dello ione ammonio e
quindi:
di questa reazione e' molto grande, perche' la
reazione e' l'inversa della ionizzazione acida dello ione ammonio e
quindi:
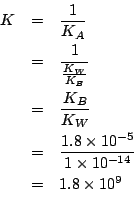
La reazione si puo' pertanto considerare completa e se ne deve determinare il reagente limitante (ovviamente, la concentrazione iniziale degli ioni idronio e' uguale a quella dell'acido cloridrico).
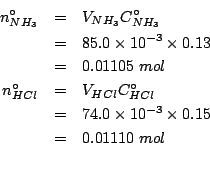
Il reagente limitante e' l'ammoniaca. Quindi:
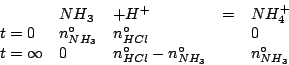
e allora:
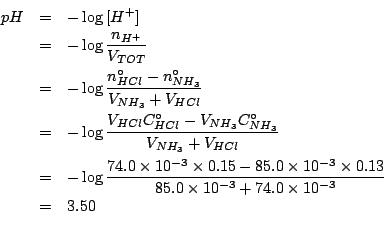
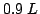 di una soluzione
di una soluzione
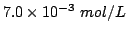 di cloruro di sodio
di cloruro di sodio
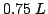 di una soluzione al
di una soluzione al 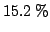 in massa di cloruro
di sodio avente densita':
in massa di cloruro
di sodio avente densita':
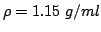 .
.
Dati:
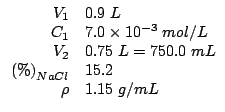
Altri simboli:
| numero di moli di |
|
| massa molare di |
|
| massa in grammi di |
|
| massa in grammi di |
Per la prima soluzione basta ricavare il numero di moli e trasformarlo nella corrispondente massa in grammi:
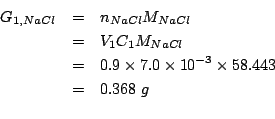
Per la seconda soluzione, basta trasformare il volume dato nella
corrispondente massa di soluzione e ricavare la massa del solo
![]() dalla percentuale:
dalla percentuale:
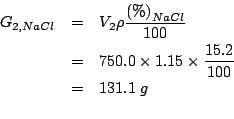
Quindi la soluzione ![]() contiene la maggior quantita' di
contiene la maggior quantita' di ![]() .
.
(Assumete che l'aggiunta del gas non cambi il volume della soluzione)
Dati:
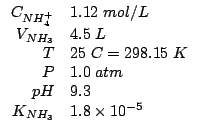
Altri simboli:
| numero di moli di ammoniaca | |
| numero di moli di ione ammonio | |
| costante dei gas:
|
Il tampone che si ottiene per aggiunta di ammoniaca ad una soluzione
di cloruro d'ammonio e' basato sulla coppia coniugata: ![]() (ovviamente, il cloruro d'ammonio e' completamente dissociato e lo
ione cloruro non ha proprieta' basiche apprezzabili). Il
(ovviamente, il cloruro d'ammonio e' completamente dissociato e lo
ione cloruro non ha proprieta' basiche apprezzabili). Il ![]() di
tale tampone e' dato da:
di
tale tampone e' dato da:
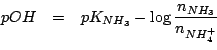
A questo punto e' sufficiente esprimere i numeri di moli in base ai
dati del problema. Rimane come unica incognita il volume
![]() della soluzione di cloruro d'ammonio, che puo' cosi'
essere determinato.
della soluzione di cloruro d'ammonio, che puo' cosi'
essere determinato.
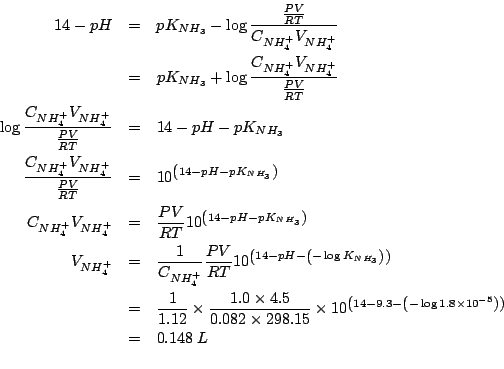
Dati:
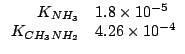
Come tutti i sali, sia il cloruro d'ammonio che il nitrato di
metilammonio sono completamente ionizzati secondo:
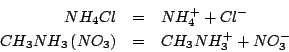
Lo ione cloruro e lo ione nitrato, essendo basi coniugate di acidi forti, non hanno proprieta' basiche apprezzabili. Lo ione ammonio e lo ione metilammonio, essendo acidi coniugati di basi deboli, hanno una forza acida non trascurabile e quindi daranno idrolisi acida.
Siccome la metilammina e' una base piu' forte dell'ammoniaca, il suo acido coniugato sara' piu' debole di quello dell'ammoniaca. Se ne conclude che, a parita' di concentrazione, sara' piu' acida la soluzione di cloruro d'ammonio.
Dati:
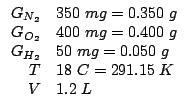
Altri simboli:
| numero di moli di azoto | |
| numero di moli di ossigeno | |
| numero di moli di idrogeno | |
| massa molare dell' azoto: |
|
| massa molare dell' ossigeno: |
|
| massa molare dell' idrogeno: |
|
| costante dei gas:
|
Scrivendo la definizione della pressione parziale di ciascun componente ed esprimendo i numeri di moli in funzione delle corrispondenti masse in grammi date, si ha:
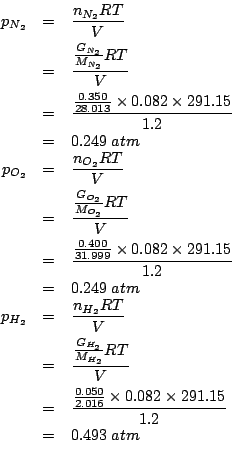
Dati:
Altri simboli:
| massa molare di |
|
| massa molare di |
|
| frazione molare dell'acqua | |
| numero di moli dell'acqua | |
| numero di moli degli ioni |
|
| numero di moli degli ioni |
|
| numero di moli di |
![]() , come tutti i sali, e' completamente ionizzato secondo:
, come tutti i sali, e' completamente ionizzato secondo:
La pressione di vapore dell'acqua nella soluzione e' legata alla sua
frazione molare, che va calcolata tenendo conto del fatto che ![]() e' completamente ionizzato:
e' completamente ionizzato:
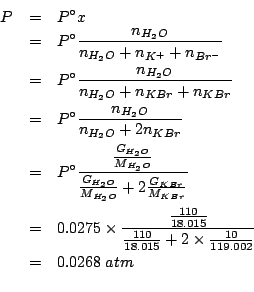
Applicando il metodo visto durante il corso si ha:
| Elettroni di valenza | |
| carica | |
| totale | |
Ponendo l'atomo di azoto (meno elettronegativo) al centro si ottengono le due formule:
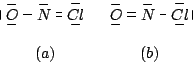
Per determinare la stabilita' relativa delle due formule di risonanza ottenute si deve valutare la carica atomica formale di ciascun atomo:
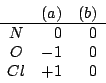
Si conclude che la formula di risonanza piu' stabile e' la
![]() .
.
Applicando il metodo visto durante il corso si ottiene:
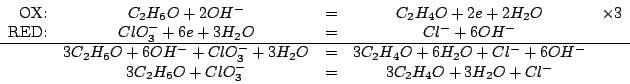
Il potenziale standard di riduzione della coppia
![]() e':
e':
![]() .
.
Dati:
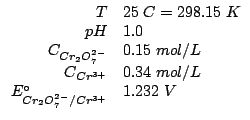
Altri simboli:
| costante dei gas:
|
|
| costante di Faraday: |
La semireazione su cui si basa il sistema elettrodico e' rappresentata da:
L'equazione di Nernst fornisce pertanto: